ekstremum Ola: Przez punkt P należący do boku pewnego trójkąta poprowadzono proste równoległe do dwóch pozostałych boków tego trójkąta i otrzymano równoległobok. W jakim stosunku punkt P powinien dzielić bok trójkąta, aby pole równoległoboku było największe?

Blee: Zapewne powinien lezec na dwusiecznej kata na przeciw tegoz boku

Ola: Nie mogę sobie z tym poradzić −.−

Blee: Zauwaz ze pole tego rownolegloku bedzie rowne: Pole duze trojkata − dwa pola malych trojkatow ktore sa do niego podobne. Wiec zadanie polega na napisaniu kiedy te dwa trojkaty (w sumie) beda mialy najmniejsze pole i tutaj juz mozesz wprowadzic skale. I wykazac ze najmniejsze pole bedzie wtedy gdy punkt D lezy na srodku boku AB.

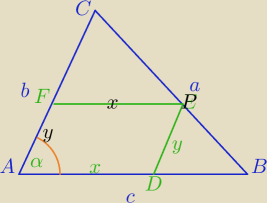
Mila: P_ADPF=x*y*sinα ΔFPC∼ΔABC

b−y		b
	=
x		c

c*b−c*y=b*x

	c
x=c−		y
	b

	c
PADPF=(c−		*y)*y*sinα
	b

	c
P(y)=(cy−		y2) sinα
	b

	−c		b
yw=		=
	c   −2*   b		2

Stąd :

CP		1
	=
PB		2

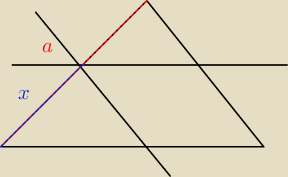
Adamm: dzieli x:(a−x) pierwszy trójkąt jest podobny w skali x, drugi w skali a1−x więc pole to P−P*(x²+(a−x)²) otrzymujemy maksimum dla x=a/2 zgodnie z pomysłem kochanusa

Adamm: poprawka pierwszy w skali x/a, drugi w (x−a)/a

	x2+(x−a)2
pole to P−P*(		)
	a2

kochanus_niepospolitus: Mila ... a nie przypadkiem

CP		1
	=
CB		2

Mila: Oczywiście masz rację, lapsus. Dziękuję. Myślę, że autorka to zauważyła.