okręgi
3h: Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne odpowiednio w punktach A,B,C.
Niech r bedzie promieniem okregu wpisanego w trójkąt ABC. Pokaż że
√3r≤2.
30 wrz 10:57
kochanus_niepospolitus:
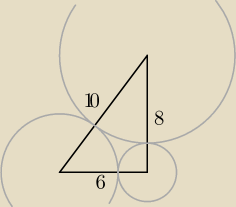
zauważ, że trójkąt o bokach 6,8,10 to trójkąt PROSTOKĄTNY (wariacja: 3,4,5).
Jaki będzie promień okręgu wpisanego w tenże trójkąt

30 wrz 11:07
kochanus_niepospolitus:
wskazówka:
wykorzystaj wzór:
30 wrz 11:09
3h: A po co mi promień okregu wpisanego w trójkąt 6,8,10

30 wrz 11:10
kochanus_niepospolitus:
Ach ... źle spojrzałem ... ma być wpisany w ABC ... a nie opisany (okrąg wpisany w pokazany
trójkąt będzie OPISANY na trójkącie ABC)
30 wrz 11:13
3h: Czy jak to rozwiązać bo już się trochę pogubiłem....
30 wrz 11:16
30 wrz 11:22
kochanus_niepospolitus:
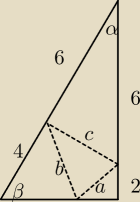
np. tak:
wyliczasz długości boków b,c,a stosując funkcje trygonometryczne dla α i β (wartości cosinusa
dla tych kątów znasz − więc jedziesz z tw. cosinusów)
Masz trzy boki trójkąta, to stosujesz wzór Herona by policzyć pole trójkąta)
Stosujesz wzór wskazany wcześniej
30 wrz 11:24
3h: A jak sprawdzić czy ta teza zachodzi w ogólnym przypadku:
Trzy okręgi o promieniach R1, R2 i R3 są parami zewnętrznie styczne odpowiednio w punktach
A,B,C. Niech r bedzie promieniem okregu wpisanego w trójkąt ABC. Pokaż że
6√3r≤R1+R2+R3.
30 wrz 14:15
Blee:
Napisze jak dojade do komputera (to pisalem ja: kochanus)
30 wrz 14:27
kochanus_niepospolitus:
Zacznijmy od końca:
| | 2PΔ | | PΔ | |
6√3r ≤ 3√3R = 3√3 |
| = 3√3* |
| |
| | 2(R1+R2+R3) | | R1+R2+R3 | |
więc należy udowodnić, że:
3
√3*P
Δ ≤ (R
1+R
2+R
3)
2
I wykazanie tego nie jest trudne, ale straaaaszliwie ślamazarne (przynajmniej jak robiłem to z
wykorzystaniem wzoru Herona).
Niestety, żadne szacowania nie wchodzą w grę, bo w ogólnym przypadku, szacowania zbytnio
windują liczbę szacującą pole trójkąta.
dochodzę do nierówności:
2[(a+b)
3 + (a+c)
3 + (b+c)
3] ≤ 11(a
3 + b
3 + c
3) + 15abc
I szczerze mówiąc nie chce mi się dalej z tym bawić
30 wrz 15:34
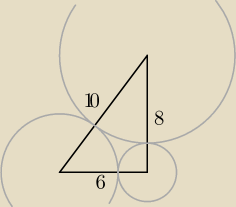 zauważ, że trójkąt o bokach 6,8,10 to trójkąt PROSTOKĄTNY (wariacja: 3,4,5).
Jaki będzie promień okręgu wpisanego w tenże trójkąt
zauważ, że trójkąt o bokach 6,8,10 to trójkąt PROSTOKĄTNY (wariacja: 3,4,5).
Jaki będzie promień okręgu wpisanego w tenże trójkąt 

 np. tak:
wyliczasz długości boków b,c,a stosując funkcje trygonometryczne dla α i β (wartości cosinusa
dla tych kątów znasz − więc jedziesz z tw. cosinusów)
Masz trzy boki trójkąta, to stosujesz wzór Herona by policzyć pole trójkąta)
Stosujesz wzór wskazany wcześniej
np. tak:
wyliczasz długości boków b,c,a stosując funkcje trygonometryczne dla α i β (wartości cosinusa
dla tych kątów znasz − więc jedziesz z tw. cosinusów)
Masz trzy boki trójkąta, to stosujesz wzór Herona by policzyć pole trójkąta)
Stosujesz wzór wskazany wcześniej