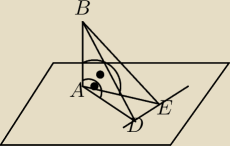
 Na płaszczyźnie π dana jest prosta DE oraz punkt A nienależący do tej prostej. Odległość punktu
A od prostej DE jest taka sama, jak odległość punktu A od punktu D i wynosi 12cm. Punk E leży
w odległości 13 cm od punktu a.. Odcinek AB jest prostopadły do płaszczyzny π, a jego długość
jest równa 16cm. Oblicz pole trójkąta BDE
Na płaszczyźnie π dana jest prosta DE oraz punkt A nienależący do tej prostej. Odległość punktu
A od prostej DE jest taka sama, jak odległość punktu A od punktu D i wynosi 12cm. Punk E leży
w odległości 13 cm od punktu a.. Odcinek AB jest prostopadły do płaszczyzny π, a jego długość
jest równa 16cm. Oblicz pole trójkąta BDE
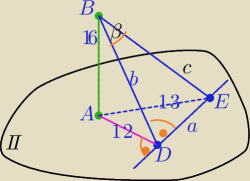 1) w ΔADE:
132=122+a2
a=5
2) W ΔBAD: AB⊥AD
b2=162+122
b=20
3) W ΔBAE: AB⊥AE
c2=162+132=425
c=5√17
4)
Sprawdzamy czy trójkąt ΔBDE jest prostokątny.
c2=425
b2+a2=400+25=425
Jest!
1) w ΔADE:
132=122+a2
a=5
2) W ΔBAD: AB⊥AD
b2=162+122
b=20
3) W ΔBAE: AB⊥AE
c2=162+132=425
c=5√17
4)
Sprawdzamy czy trójkąt ΔBDE jest prostokątny.
c2=425
b2+a2=400+25=425
Jest!
| 1 | ||
PΔBDE = | *5*20=50 | |
| 2 |