Wykaż że martin: Wykaż że równanie prostej AB gdzie A = (xA, yA) i B = (xB, yB) oraz xA ≠ xB można zapisać w postaciach. y − yA = ^{yB − yA}_{xB − xA} * (x − xA) oraz (y − yA) * (xB − xA) − (yB − yA) * (x − xA) = 0. Macie jakiś pomysł jak to zrobić? Albo chociaż jak się do tego zabrać?

Milo: Niech prosta AB będzie miała postać kierunkową y = ax + b (a ma, bo x_A≠x_B) Wówczas spełniają to równanie współrzędne punktów A,B: y_A = ax_A + b y_B = ax_B + b Odejmując stronami: y_A − y_B = a(x_A − x_B)

	yA − yB
a =
	xA − xB

To jeszcze raz: Równanie prostej:

	yA − yB
y =		x + b
	xA − xB

punkt A na niej

	yA − yB
yA =		xA + b
	xA − xB

Odejmując stronami otrzymujemy:

	yA − yB
y − yA =		(x − xA)
	xA − xB

Stąd do drugiej postaci przejść już łatwo

Milo:

	yA − yB		yB − yA
Bo oczywiście		=
	xA − xB		xB − xA

Krzysiek:

martin: Rzeczywiście. Dzięki wielkie

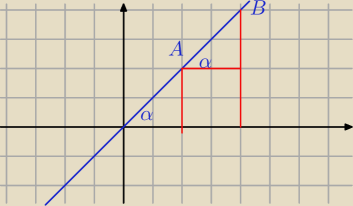
Janek191: A = (x_A, y_A) B = ( x_B, y_B) x_A ≠ x_B y =a x + b

	yB − yA
a = tg α =
	xB − xA

więc

	yB − yA
y =		*X + b − przechodzi przez punkt A = ( XA , yA)
	xB − xA

więc

	yB − yA
yA =		* XA + b
	xB − xA

to

	yB − yA
b = yA −		* xA
	xB − xA

czyli

	yB − yA		yB − yA
y =		*x + yA −		* xA
	xB − xA		xB − xA

	yB − yA
y − yA =		*( x − xA)
	xB − xA

===================================