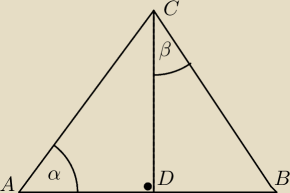
Kat dwa razy wiekszy Krzysiek: W trojkacie rownoramiennym kąt A jest katem przy wierzcholku trojkata Z wierzcholka C wykreslcie wysokosc CD wzgledem boku AB Udowodnic ze kat A jest dwa razy wiekszy od kata BCD α=2β

wiesiu: Wiemy co jest ramionami a co podstawą?

a: kątem przy wierzchołku trójkąta Z wierzchołka C

wiesiu: Właśnie tego nie rozumiem w zadaniu

Krzysiek: ..... trojkata. Z wierzcholka C......

Krzysiek: Rysunek nalezalo sobie zrobic samaemu

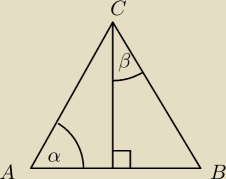
wiesiu: α+β=90 Załóżmy że α=45^o Wtedy β=45^o α=β co jest sprzeczne z założeniem Oczywiście jest to pierwszy przypadek

Krzysiek: Pomysle

wiesiu:

α
	+90o−β=90
2

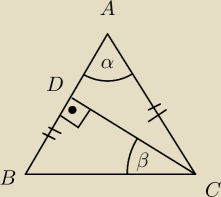
α=2β ckd I drugi przypadek

Krzysiek: Co zrobiles? ale dokladnie

Krzysiek: Wybacz mam dzisiaj duzy kloppt z laczem . Wiec na teraz sobie daruje zadania .

wiesiu: Kąt przy punkcie B jest równy 90^o−β ponieważ 180^o=β+B+90 Kąt przy punkcie A podzieliłem na pół => α/2 I sprawdzam czy suma tych kątów da 90^o

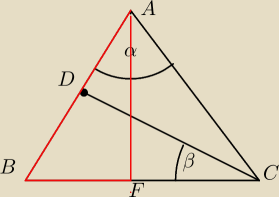
Krzysiek: Moze uda sie to wyslac Poprowadzilem dwusieczna kąta α jak sugerowales Wiec AB⊥DC AF⊥BC

	1
Wiec z twierdzenia o rownosci kątow o raminach odpowiednio prostopadlych ∡		α=β
	2

Stad α= 2β Nie wiem czy tak moze byc

RNJ: jak dokładnie brzmi "twierdzenie o równości katów o ramionach odpowiednio prostopadłych"? wniosek że α = 2β przy takim rysunku zachodzi tylko dla Δ równobocznego

wiesiu: Tylko w pierwszym przypadku który narysowałem

Krzysiek: Jesli dwa kąty maja ramiona odpowiednio prostopadle to kąty te sa rowne (jesli oba sa ostre lub rozwarte)

wiesiu: W sensie do zdania "wniosek że α = 2β przy takim rysunku zachodzi tylko dla Δ równobocznego"

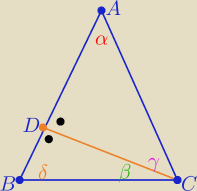
Eta: 90^o=δ+β=γ+α i β+γ=δ zatem β+γ+β=γ+α ⇒ α= 2β ======

Krzysiek: Dzieki Eta duzo pracy bede mial

Eta: Witam A nad czym tak "pracujesz"?

Krzysiek: Witam rowniez Teraz okregi i pozniej miejsca geometryczne ale tez wzialem zadania ze starej ksiazki do geometrii (przed okregami

Krzysiek: Witam rowniez Teraz okregi i pozniej miejsca geometryczne ale tez wzialem zadania ze starej ksiazki do geometrii (przed okregami