rozwiąż nierówność
matematycznyswir: rozwiąż nierówność cos2x−3sinx+3/4>0 przy założeniu, że 0<x<2n.
25 wrz 22:06
Jerzy:
cos2x = 1 − sin2x
25 wrz 22:17
matematycznyswir: i co dalej?
25 wrz 22:22
Milo: | | 3 | |
1 − sin2x − 3sinx + |
| > 0 |
| | 4 | |
| | 7 | | 1 | | 7 | |
(sinx + |
| )(sinx − |
| ) < 0 /:(sinx + |
| ) >0 w ℛ (dlaczego?) |
| | 2 | | 2 | | 2 | |
25 wrz 22:25
'Leszek: Postaw: sin x = t , t ε R
1 − t2 −3t +(3/4) >0 ⇔ t2 + 3t − ( 7/4) < 0 i rozwiaz .....
25 wrz 22:26
'Leszek: Sorry , powinno byc : t ε [ −1 , 1 ]
25 wrz 22:30
matematycznyswir: nie było mnie wtedy i nie mam pojęcia dalej jak to zrobić do samego końca
25 wrz 22:32
Milo: | | 1 | |
Narysuj wykres i odczytaj, kiedy sinx < |
| |
| | 2 | |
25 wrz 22:39
Janek191:
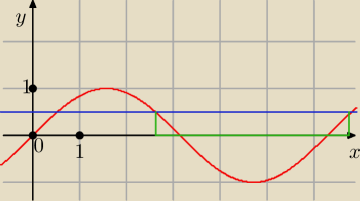
sin x < 0,5
x ∊ ( 150
o + k*360
o, 390
o + k*360
o ) , k − dowolna liczba całkowita
Zapisz kąty w mierze łukowej.
26 wrz 07:23