Ktoś pomoże? Problem: Wielomian x³+px+q ma 3 pierwiastki rzeczywiste, udowodnij że p<0 Ktoś ma jakiś pomysł?

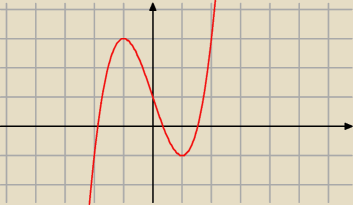
Janek191: w(x) = x³ − 3 x + 1 w(x) = x³ + p x + q w'(x) = 3 x² + p = 0 ⇔ p < 0 Funkcja w(x) musi mieć maksimum i minimum lokalne, aby miała 3 miejsca zerowe.

Problem: Dzięki, wszystko jasne!

Milo: Ze wzorów Viete'a 0 = x₁ + x₂ + x₃ p = x₁x₂ + x₁x₃ + x₂x₃ Pierwsze z tych równań do kwadratu, dostaniemy 0 = x₁² + x₂² + x₃² + 2p

	x12 + x22 + x32
Skąd p = −		< 0 przy założeniu, że wszystkie 3 pierwiastki nie są
	2

jednocześnie zerami

bitter: Milo, fajny pomysł. Ale zastanawiam się czy to, że suma pierwiastków jest równa zero jest oczywiste?

Milo: Tak, bo współczynnik przy x² jest równy 0

mat: to wynika z tego, że nie ma członu x²

bitter: ah, no rzeczywiście, dzięki

zombi: Wymnóż (x−x₁)(x−x₂)(x−x₃), wtedy wzory Viete'a dla wielomianów przestają być tajemnicą, naprawdę

karty do gry : w(x) = x³ + px + q Jeśli p ≥ 0 to w(x) jest sumą jednej funkcji niemalejącej oraz dwóch rosnących. Taka suma jest funkcją rosnącą, więc może przeciąć oś OX tylko w jednym punkcie.Musi być p < 0. Warunek wystarczający na 3 różne miejsca zerowe wygląda następująco:

	p		q
(		)3 + (		)2 < 0
	3		2