Sinus Stos: Cześć, Jak udowodnić, że okresem funkcji sin² jest π?

Bogdan:

	1		1
cos(2α) = 1 − 2sin2α ⇒ sin2α =		−		cos(2α)
	2		2

Trzeba wyznaczyć okres funkcji f(x) = cos(2α)

Stos: okres cos(2α) to π. I co dalej?

Bogdan: a dalej to już samodzielnie kontynuuj

Mila: f(x)=sin²x

	1
f(x)=		*(1−cos(2x))
	2

1) sposób okres funkcji cosx to 2π

	2π
T=		=π −okres funkcji cos(2x)
	2

II sposób z definicji f(x)=f(x+T)=f(x−T), T jest stałą i T niezależna od x

1		1
	*(1−cos(2x))=		*(1−cos(2x−2T))⇔
2		2

1−cos(2x)=1−cos(2x−2T)⇔ cos(2x)=cos(2x−2T) 2x=2x−2T+2kπ lub 2x=−2x−2T+2kπ 2T=2kπ lub 4x=−2T+2π ( T zależne od x) T=π,

Stos: ok, jednakże mam pytanie, czy na tym etapie mogę stwierdzić że okresem sin²jest π, ponieważ okresem tego ^1−cos(2α)₂ jest π

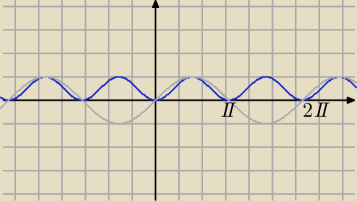
Mila: Tak, ponieważ :

	1
sin2x=		*(1−cos(2x))
	2