Graniastosłup prawidłowy sześciokątny.
domka09: Zbiornik ma kształt graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy 0,6m.
Najdłuższa przekątna graniastosłupa jest trzy razy dłuższa od najkrótszej przekątnej podstawy.
Zbiornik napełniono wodą do wysokości 0,2m.
a) Oblicz stosunek objętości wody do objętości graniastosłupa.
b) O ile procent objętość pustej części zbiornika jest większa od objętości wody?
Proszę o pomoc, mam problem z dojściem do poprawnego wyniku
Janek191:
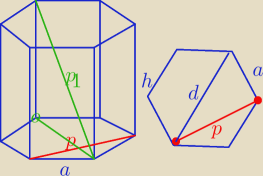
Mamy
a = r = 0,6 m
d = 2 a = 1,2 m
p
2 + a
2 = d
2 ⇒ p
2 = 1,2
2 − 0,6
2 = 1,44 − 0,36 = 1,08 = 3*0,36
p = 0,6
√3
zatem
p
1 = 3 p = 1,8
√3
oraz
h
2 + d
2 = (p
1)
2
h
2 = (1,8
√3)
2 − 1,2
2 = 3,24*3 − 1,44 = 8,28
h =
√8,28
Objętość wody
| | a2 √3 | |
Vw = Pp*h1 = |
| *0,2 = 0,018 √3 [ m3] |
| | 4 | |
Objętość zbiornika ( graniastosłupa)
| | a2 √3 | |
Vg = Pp*h = |
| *√8,28 = 0,09 √3*√8,28 = ... |
| | 4 | |
Dokończ