Figury na plaszczyznie kartezjańsiej kobus: Z punktu A poprowadzono styczne do okręgu o. Oblicz długość każdego z odcinków wyznaczonych przez punkt A i punkt styczności, gdy: A = (0, −4) i o: x² + y² − 10x + 2y + 10 = 0. Proszę o rozwiązanie tego przykładu; pozostałe podpunkty robię bez problemu − tu jest coś nie tak i nie zgadza mi się z odpowiedzią − √34

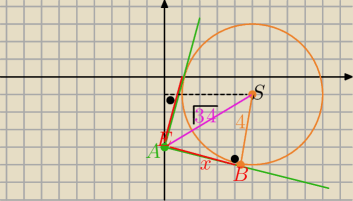
Eta: S( 5,−1) , r=4 |AS|=....= √34 to x= √34−4²=√18=3√2