trygonometria
paulina: Wiedząc, że tgα=1/3 oblicz wartość wyrażenie 5(2sin2α−1).
28 sty 14:44
Mariusz: | | sinα | | 1 | |
tgα= |
| = |
| →cosα=3sinα
|
| | cosα | | 3 | |
5(2sin
2α−1)=5(2sin
2α−sin
2α−cos
2α)=5(sin
2α−cos
2α)=5(sinα+cosα)(sinα−cosα)
dalej nie mam pomysłu

28 sty 15:02
Mariusz: pomagam już wiem

28 sty 15:07
Mariusz: | | tgα | | tg2α | | 1 | |
sin2α= |
| = |
| = − |
| |
| | tgα−ctgα | | tg2α−1 | | 80 | |
28 sty 15:09
paulina: dzięki wielkie

28 sty 15:42
paulina: ale ma wyjść −4

28 sty 15:44
walet:
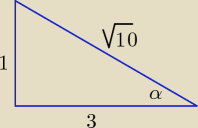
| | 1 | | 1 | |
sinα = |
| , sin2α = |
|
|
| | √10 | | 10 | |
| | 1 | | 10 | |
5*(2 * |
| − 1) = |
| − 5 = −4
|
| | 10 | | 10 | |
i to wszystko

28 sty 15:49
paulina: dzieki

28 sty 15:55






