pochodna funkcji w punkcie
kasia123: Jak rozpoznać z rysunku, że funkcja nie ma pochodnej w jakimś punkcie? Czy wtedy ta funkcja nie
jest ciągła

Kiedy trzeba badać granicę prawo− i lewostronną?
25 wrz 13:54
'Leszek: funkcja f(x) = | x −1 | nie ma pochodnej w punkcie x = 1 , chociaz w x= 1 jest ciagla,
nalezy obliczyc pochodna lewostronna i prawostronna .
Jezeli f '−(x) ≠ f '+(x) to funkcja nie ma pochodnej w punkcie x
25 wrz 14:18
zombi: Chodzi głównie o "kształt" funkcji. Jeśli ma wystające, ostre zęby jak np. podana przez
Leszka wartość bezwzględna |x−1| w punkcie x=1, to nie będzie tam pochodnej.
25 wrz 14:22
Milo: Warunkiem koniecznym różniczkowalności funkcji w punkcie jest ciągłość, więc tak − jeśli
funkcja w jakimś punkcie nie jest ciągła, to na pewno nie ma w nim pochodnej.
Ale to nie wszystko, weźmy np. funkcję f(x) = |x|
Mimo że jest ciągła w ℛ, nie ma pochodnej w x0=0
Właśnie takie "ostre zakończenia" funkcji też świadczyć mogą o tym, że nie ma ona tam pochodnej
I tak średnio może to robić za dowód − lepiej badać ciągłość i pochodne lewo− i prawostronne
25 wrz 14:22
kasia123: jak mam obliczyć lewo− i prawostronną granicę w podanym przez Leszka przykładzie? Nie miałam w
szkole tego wzoru z h dążącym do zera. Czy jest inna droga?
25 wrz 15:13
Mila:
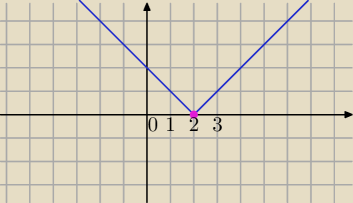
w x=2 − nie ma pochodnej
25 wrz 15:29
Mila:
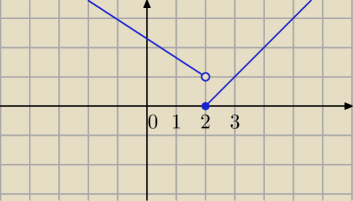
w x=2 nie ma pochodnej
A zatem w "szpicach" i "urwiskach".
25 wrz 15:32
kasia123: Dziękuję
25 wrz 15:33
'Leszek: @Mila , ale w "szpicu " funkcja jest ciagla, a w "urwisku " nie !
25 wrz 15:41
Mila:
Zgadza się. Dlatego w w urwisku nie liczymy granicy ilorazu różnicowego.
25 wrz 15:50
 Kiedy trzeba badać granicę prawo− i lewostronną?
Kiedy trzeba badać granicę prawo− i lewostronną?
 w x=2 − nie ma pochodnej
w x=2 − nie ma pochodnej
 w x=2 nie ma pochodnej
A zatem w "szpicach" i "urwiskach".
w x=2 nie ma pochodnej
A zatem w "szpicach" i "urwiskach".