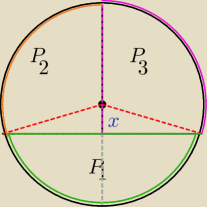
 Tworzymy okrąg o promieniu R, prowadzimy średnicę, następnie prowadzimy prostopadłą cięciwę do
poprowadzonej średnicy, usuwamy (szarą) część zaznaczoną na rysunku. Tworzą nam się trzy Pola
zaznaczone mniej więcej na rysunku (różowe, zielone i pomarańczowe). Polecenie jest takie aby
wyznaczyć takie x (odległość cięciwy od środka okręgu − x) aby pola P1, P2 i P3 były równe.
Czy w ogóle taka sytuacja jest możliwa?
Tworzymy okrąg o promieniu R, prowadzimy średnicę, następnie prowadzimy prostopadłą cięciwę do
poprowadzonej średnicy, usuwamy (szarą) część zaznaczoną na rysunku. Tworzą nam się trzy Pola
zaznaczone mniej więcej na rysunku (różowe, zielone i pomarańczowe). Polecenie jest takie aby
wyznaczyć takie x (odległość cięciwy od środka okręgu − x) aby pola P1, P2 i P3 były równe.
Czy w ogóle taka sytuacja jest możliwa?
| 1 | 1 | |||
P2=P3= | αR2+ | PΔ | ||
| 2 | 2 |
| 1 | ||
PΔ= | *sin(−2α)*R2 | |
| 2 |
| 1 | 1 | |||
(π−α)*R2−PΔ= | αR2+ | PΔ | ||
| 2 | 2 |
| x | ||
cos(α−π)= | ||
| R |