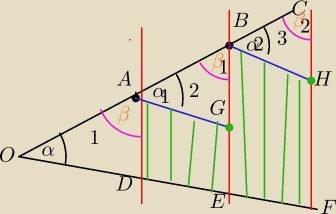
Dowod (kąt i proste rownolegle 5-latek: Dane sa dwie polproste o wspolnym poczatku nie zawarte w jednej prostej na jednej z polprostych odlozono 3 odcinki rownej dlugosci i przez konce tych odcinkow poprowadzono proste rownolegle w taki sposob ze przecinaja one druga polprosta Udowodnij ze odcinki wyznaczone na drugiej polprostej sa rownej dlugosci zalozenie OA=AB =BC ADIIBEIICF Teza OD=DE=EF Dowod Dla dowodu wykreslmy z punktow A i B rownolegle do OF odcinki AG i BH mam trzy trojkaty ΔOAD ΔABG ΔBCH ΔOAD ≡ΔABG na podstawie cechy KBK bo OA=AB z zalozenia ∡α=α₁ ∡β= ∡β₁ Jako katy odpowiadajace i przylegle do tych bokow Na tej samej podstawie ΔABG≡BCH i ΔOAD≡BCH Z przystawania tych trojkatow wynika ze OD=AG=BH Ale AG=DE jako przeciwlegle boki w rownolegloboku AGDE iBH=EF jako przeciwlegle boki w rownolegloboku BHEF Stad OD= DE=EF

RadkNieJadek: krótkie sposoby: 1/ skorzystać z tw.Talesa 2/ skorzystać z podobieństwa trójkątów: ΔOAD ΔOBE ΔOCF (kkk), potem skala podobieństwa

5-latek: Radek z Talesem chetnie bym sie poznal Masz moz enr telefonu do niego?

RadkNieJadek: on już w krainie Hadesa, a to obszar bez zasięgu

5-latek:

Mila: