 Na dzisiaj takie zadanko
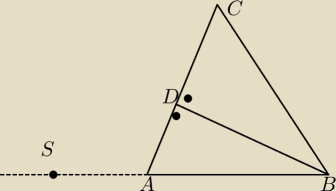
Dany jest trojkat rownoramienny ABC w ktorym AC=BC
Na przedluzeniu podstawy wybrano dowolnie punkt S
Udowodnij z e wartosc bezwzgledna roznicy odlegoci punktu S od prostch AC i BC jest rowna
dlugosci wysokosci tego trojklata poprowadzonej z wiezcholka B
|SA−SB|= BD
Nie wiem jak zaczac (pewnie trzeba cos dorysowac
Na dzisiaj takie zadanko
Dany jest trojkat rownoramienny ABC w ktorym AC=BC
Na przedluzeniu podstawy wybrano dowolnie punkt S
Udowodnij z e wartosc bezwzgledna roznicy odlegoci punktu S od prostch AC i BC jest rowna
dlugosci wysokosci tego trojklata poprowadzonej z wiezcholka B
|SA−SB|= BD
Nie wiem jak zaczac (pewnie trzeba cos dorysowac
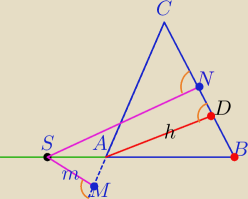 |SN−SM|=h
|SN−SM|=h
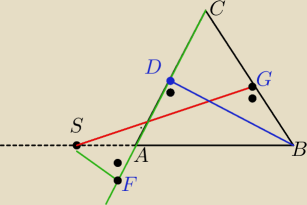 Leszsek nie AB tylko BD (wysokosci
Wiec bedzie to inaczej
|SF−SG|= BD
Leszsek nie AB tylko BD (wysokosci
Wiec bedzie to inaczej
|SF−SG|= BD
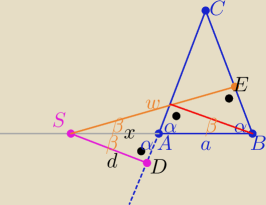 Dwa razy z podobieństwa trójkątów prostokątnych
ΔADS i ABF oraz BES i ADS
Dwa razy z podobieństwa trójkątów prostokątnych
ΔADS i ABF oraz BES i ADS
| a | h | w | a+x | a | |||||
= | oraz | = | = | +1 | |||||
| x | d | d | x | x |
| w | h | |||
zatem | = | +1 /*d>0 | ||
| d | d |

 Wysokosc z wierzcholka B
Ale dlatego narysowalas z wierzcholka A bo sa one rownej dlugosci wtym trojkacie ?
Wysokosc z wierzcholka B
Ale dlatego narysowalas z wierzcholka A bo sa one rownej dlugosci wtym trojkacie ?
 Podobienstwo jest w klasie 2 ja jestem teraz w 1 klasie i rozdzial [C[ Kąty przy prostych
rownoleglych przecietych sieczna ]]
Podobienstwo jest w klasie 2 ja jestem teraz w 1 klasie i rozdzial [C[ Kąty przy prostych
rownoleglych przecietych sieczna ]]



