dwusieczne kątow przyleglych
5-latek:
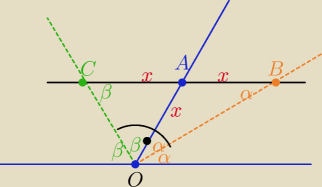
W katach przyleglych α i β poprowadzono dwusieczne
Przez punkt A lezacym na wspolnym ramieniu tych kątow poprowadzono prosta rownolegla do
pozostalych ramion
prosta ta przecina dwusieczna kąta α w punkcie B i dwusieczna kąta β w punkcie C
Udowodnij ze AB=AC
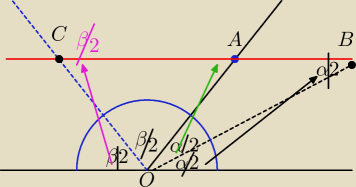
ΔCOB to trojkat prostokatny bo β/2+α/2=90
o
Kąt ABO ma miare α/2 jako kąt naprzemian legly wewnetrzny
Z rownosci tych katow wynika ze trojkat OAB jest rownoramienny czyli OA=AB
Kąt ACO = β/2
Kąt CAO= α/2
α/2= 90−β/2
Nie wiem jak wykazac ze CA=OA
5-latek: Boże jak ja patrzylem na ten trojkat
Wynika z tego ze ΔCOA jest rownoramienny i OA=CA
ale tez OA= AB wiec AB=CA
