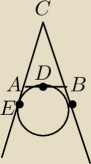
Trójkąt srki: Wiemy, że 3AC=AB+BC. Trzeba udowodnić że CDE to kat prosty.

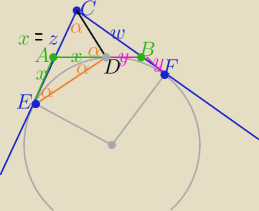
Eta: 1/ Przejrzysty rysunek! 2/ z twierdzenia o odcinkach stycznych |EA|=|AD|=x i |DB|=|BF|=y oraz |EC|=|FC| ⇒ x+z=y+w 3/ z treści zadania: 3z=x+y+w ⇒ 3z=x+x+z ⇒ z=x to w trójkącie EDC AD=x jest środkową zatem ΔEDC jest prostokątny o kącie prostym przy wierzchołku D zatem |<CDE|=90^o lub tak : Mamy podział trójkąta EDC na dwa trójkąty równoramienne (AED i ADC o równych kątach α przy podstawach to wΔEDC 4α=180^o ⇒ 2α=90^o = |<EDC| =========== c.n.w

RadekNieJadek: @ [PEta]] dlaczego kąty przy podstawach w ΔAED są równe kątom przy podstawach w ΔADC? oba trójkąty są równoramienne, ale czy mają takie same miary kątów?

Eta: Ajjjj ... mają być α,α i β, β wtedy 2α+2β=180^o ⇒ α+β=90^o=|<EDC| Źle oznaczyłam i tak napisałam patrząc na rysunek Dzięki za poprawkę