Wytłumaczy ktoś?
Mary: Jak to zrobić punkt po punkcie?
Dany jest okrąg o środku O i promeniu R oraz okrąg o środku S i promieniu r. Podaj liczbę
punktów wspólnych tych okręgów w zależności od R.
a) |OS|=4, R=1
Wyliczylam juz, ze r = 3
No i ze gdy r<3 to mamy 0 punktów wspólnych. Ale reszty nie potrafię. Nie umiem używać tych
wzorów. Może mi ktoś wytłumaczyć jak sie to robi?
23 wrz 14:25
Pytający:
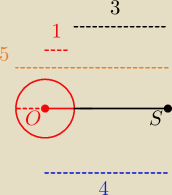
Wzajemne położenie okręgów:
473
Patrz rysunki z linku i rysunek tu.
Dla:
r<3 mamy okręgi rozłączne zewnętrznie, 0 punktów wspólnych,
r=3 mamy okręgi styczne zewnętrznie, 1 punkt wspólny,
3<r<5 mamy okręgi przecinające się 2 punkty wspólne,
r>5 mamy okręgi rozłączne wewnętrznie, 0 punktów wspólnych.
23 wrz 16:07
5-latek: Czesc.
Ale napisano w zaleznosci od R
23 wrz 16:09
Mary: Ale jak to z wzorów obliczyć?
23 wrz 16:18
Pytający:
Cześć, ale R nie podano, natomiast r owszem.

A jak ze wzorów? Ano podstawić.
Np. w podesłanym linku masz wzór:
Okręgi przecinające się, gdy |r
1−r
2|<|AB|<r
1+r
2,
co po podstawieniu wygląda:
|R−r|<|OS|<R+r
|1−r|<4<1+r
Masz dwie nierówności, wystarczy je rozwiązać (pamiętając, że r>0):
1.
|1−r|<4
1−r<4 ⋀ −(1−r)<4
r>−3 ⋀ r<5
r>0 ⋀ r<5 // bo r>0
2.
4<1+r
r>3
1. ∧ 2.
(r>0 ⋀ r<5) ∧ (r>3)
3<r<5
itp.
23 wrz 16:38
RadekNieJadek:
Mary napisała, że R=1, a r wyliczyła sama
pewnie jest błąd w przepisaniu polecenia i trzeba analizować w zależności od r, bo r wyliczone
za szybko
23 wrz 17:06
Pytający:
Oczywiście chciałem napisać na odwrót, czyli: "r nie podano, natomiast R owszem".
23 wrz 17:21
 Wzajemne położenie okręgów: 473
Patrz rysunki z linku i rysunek tu.
Dla:
r<3 mamy okręgi rozłączne zewnętrznie, 0 punktów wspólnych,
r=3 mamy okręgi styczne zewnętrznie, 1 punkt wspólny,
3<r<5 mamy okręgi przecinające się 2 punkty wspólne,
r>5 mamy okręgi rozłączne wewnętrznie, 0 punktów wspólnych.
Wzajemne położenie okręgów: 473
Patrz rysunki z linku i rysunek tu.
Dla:
r<3 mamy okręgi rozłączne zewnętrznie, 0 punktów wspólnych,
r=3 mamy okręgi styczne zewnętrznie, 1 punkt wspólny,
3<r<5 mamy okręgi przecinające się 2 punkty wspólne,
r>5 mamy okręgi rozłączne wewnętrznie, 0 punktów wspólnych.
 A jak ze wzorów? Ano podstawić.
Np. w podesłanym linku masz wzór:
Okręgi przecinające się, gdy |r1−r2|<|AB|<r1+r2,
co po podstawieniu wygląda:
|R−r|<|OS|<R+r
|1−r|<4<1+r
Masz dwie nierówności, wystarczy je rozwiązać (pamiętając, że r>0):
1.
|1−r|<4
1−r<4 ⋀ −(1−r)<4
r>−3 ⋀ r<5
r>0 ⋀ r<5 // bo r>0
2.
4<1+r
r>3
1. ∧ 2.
(r>0 ⋀ r<5) ∧ (r>3)
3<r<5
itp.
A jak ze wzorów? Ano podstawić.
Np. w podesłanym linku masz wzór:
Okręgi przecinające się, gdy |r1−r2|<|AB|<r1+r2,
co po podstawieniu wygląda:
|R−r|<|OS|<R+r
|1−r|<4<1+r
Masz dwie nierówności, wystarczy je rozwiązać (pamiętając, że r>0):
1.
|1−r|<4
1−r<4 ⋀ −(1−r)<4
r>−3 ⋀ r<5
r>0 ⋀ r<5 // bo r>0
2.
4<1+r
r>3
1. ∧ 2.
(r>0 ⋀ r<5) ∧ (r>3)
3<r<5
itp.