calka oni: Oblicz pole ograniczone funkcjami:

	3
y1=√3x x=4 y2=
	x2

y₁=y₂ jakie wyjde z tego warunki? nie potrafie tego rozpisac

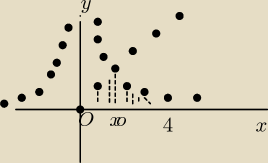AS: Wyznaczam punkt wspólny krzywej i prostej

	3		3
√3*x =		⇒ x3 =		= √3 = x = 3√√3 = 6√3
	x2		√3

xo = ⁶√3 Szukane pole składa się z dwóch obszarów pod prostą w <0,xo> i krzywą w <xo,4>

	x2		√3		√3
P1 = ∫oxo(√3*x)dx = √3*		|oxo =		*(xo2 − 02} =		*xo2
	2		2		2

	3		x−1		−3
P2 = ∫xo4(		)dx = ∫xo4(3*x−2)dx = 3*		|xo4 =		|xo4
	x2		−1		x

	−3		−3		−3		3
P2 =		−		=		+
	4		xo		4		xo

Szukane pole

	√3		3		3
P = P1 + P2 =		*xo2 +		−
	2		xo		4

oni: a no tak. ja probowalem automatycznie odejmowac funkcje od sibie i potem wynik calkowac. dziekuje bardzo za rozjasnienie umyslu