Szeregi
amm: ∞
n=1
| | n2+1 | | 1 | |
ln( |
| )=ln(1+ |
| )→ln1=0 |
| | n2 | | n2 | |
to wystarczy, żeby stwierdzenie zbieżności szeregu?
22 wrz 00:51
Adamm: nie
to warunek konieczny
jak nazwa wskazuje, konieczny, ale nie wystarczający
22 wrz 00:55
amm: tak myślałem, pomożesz dalej? nie wiem, jakim kryterium bym się mógł z tym uporać
22 wrz 01:07
Adamm: | | 1 | |
t/(1−t)>ln( |
| ) dla 0<t<1 |
| | 1−t | |
| 1 | | n2+1 | |
| >ln( |
| ) więc szereg z kryterium porównawczego zbieżny |
| n2 | | n2 | |
22 wrz 01:18
Adamm:
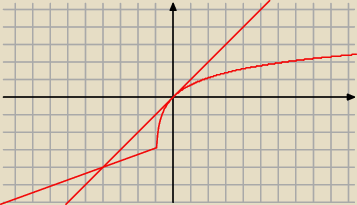
jest też taka nierówność
ln(1+x)≤x dla x>−1
bardziej adekwatna do sytuacji
22 wrz 01:21
Adamm: rysunki się czasami psują na forum, ale tam miał być ln(1+x)
22 wrz 01:21
amm: Wszystko jasne, dzięki wielkie!
22 wrz 01:44