trojkat i wysokosc
5-latek:
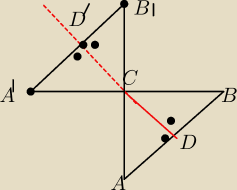
W trojkacie ABC w ktorym kat C jest prosty przedluzono bok AC poza punkt C do punktu B'
takiego ze
CB'= CB
oraz bok BC poza punkt C do punktu A' takiego ze CA'= CA
Mamy udowodnic ze przedluzenie wysokosci CD trojkata ABC jest srodkowa w trojkacie A'B'C
Zeby przedluzenie wysokosci CD bylo srodkowa ΔA'B'C to musimy udowqadnic ze D'C= A'D'= D'B'
srodkowa w trojkacie prostokatnym dzieli ten trojkat na dwa troklaty rownoramienne
na razie zbieram fakty .
jesli ktos dorzuci cos jeszcze to bedzie lepiej

21 wrz 23:40
5-latek: Z tresci zadania wiemy zeΔABc≡A'B'C (na podsatwie cechy BKB
∡CAB=α
∡CBA= 90o−α
∡ACD= 90−α
∡B'CD'= 90o−α (jako wierzcholkowy
∡BCD=α
∡D'CA'=α jakio wierzcholkowy
∡B'A'C=α
∡A'B'C= 90o−α
W trojkacie A'D'C mamy dwa jednakowe katy α
To oznacza z etrojkat jest rownoramienny czyli D'C= A'D'
W trojkacie B'D'C mamy dwa jednakowe katy (90o−α) z to oznacza ze trojkat jest rownoramienny
czyli D'C=D'B'
Z rownosci tych wynika Δ A'B'c jest trojkatem prostokatnym rownoramiennym wiec przedluzenie
wysokosci CD trojkata ABC
jest srodkowa w trojkacie A'B'C .
22 wrz 13:00
Tadeusz:
... co nie to nie

22 wrz 13:07
Jerzy:
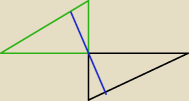
Czegoś tutaj nie rozumiem.
22 wrz 13:09
Tadeusz:
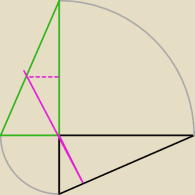
podpowiedź

22 wrz 13:14
Jerzy:
Teraz mi się wszystko zgadza

22 wrz 13:17
Eta:
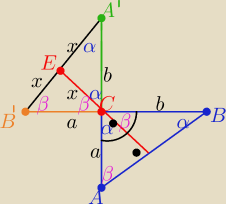
22 wrz 13:18
Tadeusz:
Najtrudniejsze są rzeczy oczywiste. Załapał, że ma trójkąty równoramienne a żabka nie kuma
że wysokość w trójkącie równoramiennym dzieli podstawę na połowy.
22 wrz 13:18
5-latek: Dzien dobry [Eta]]

dziekuje za rysunek .
Tadeusz Witaj

. trudno zobaczyc żolte .
Wlasnie zaraz ide do pracy i
duch puszczy mi to podpowiedzial zebym w pracy nie myslal o
tym

22 wrz 13:23
 W trojkacie ABC w ktorym kat C jest prosty przedluzono bok AC poza punkt C do punktu B'
takiego ze
CB'= CB
oraz bok BC poza punkt C do punktu A' takiego ze CA'= CA
Mamy udowodnic ze przedluzenie wysokosci CD trojkata ABC jest srodkowa w trojkacie A'B'C
Zeby przedluzenie wysokosci CD bylo srodkowa ΔA'B'C to musimy udowqadnic ze D'C= A'D'= D'B'
srodkowa w trojkacie prostokatnym dzieli ten trojkat na dwa troklaty rownoramienne
na razie zbieram fakty .
jesli ktos dorzuci cos jeszcze to bedzie lepiej
W trojkacie ABC w ktorym kat C jest prosty przedluzono bok AC poza punkt C do punktu B'
takiego ze
CB'= CB
oraz bok BC poza punkt C do punktu A' takiego ze CA'= CA
Mamy udowodnic ze przedluzenie wysokosci CD trojkata ABC jest srodkowa w trojkacie A'B'C
Zeby przedluzenie wysokosci CD bylo srodkowa ΔA'B'C to musimy udowqadnic ze D'C= A'D'= D'B'
srodkowa w trojkacie prostokatnym dzieli ten trojkat na dwa troklaty rownoramienne
na razie zbieram fakty .
jesli ktos dorzuci cos jeszcze to bedzie lepiej 

 Czegoś tutaj nie rozumiem.
Czegoś tutaj nie rozumiem.
 podpowiedź
podpowiedź 


 dziekuje za rysunek .
Tadeusz Witaj
dziekuje za rysunek .
Tadeusz Witaj . trudno zobaczyc żolte .
Wlasnie zaraz ide do pracy i duch puszczy mi to podpowiedzial zebym w pracy nie myslal o
tym
. trudno zobaczyc żolte .
Wlasnie zaraz ide do pracy i duch puszczy mi to podpowiedzial zebym w pracy nie myslal o
tym 