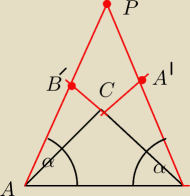
Trojkat Powracający: W trojkacie ABC poprowadzono wysokosci AA'i BB' proste zawierajace te wysokosci przcinaja sie w punkcie P Udowodnij ze jezeli AP=PB to trojkat ABC jest rownoramienny Autor zrobil taki rysunek do zadania Przeciez rysyjac trojkat ostrokatny wysokosci przecinaja sie wewnatrz trojkata

Blee: No a gdzie sie przecinaja jak nie wewnatrz trojkata?

Tadeusz: Rysunek jest trochę spaprany. Wysokości trójkąta przecinają się oczywiście w jednym punkcie a punkt ten może "leżeć" zarówno wewnątrz jak i na zewnątrz trójkąta.

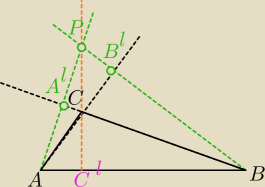
Tadeusz: Proste zawierające wysokości AA' i BB' trójkąta ABC przecinają się w punkcie P Zatem prosta zawierająca wysokość CC' tego trójkąta również przechodzi przez punkt P Skoro trójkąt APB jest równoramienny (AP=BP) to jego wysokość PC' dzieli bok AB na połowy Skoro wysokości CC' i PC' leżą na jednej prostej to trójkąt ABC musi być równoramienny (AC=BC)

5-latek: dzieki kolego .

5-latek: Tez mialem takie zadanie (nr 57 Maria Malek cz 1 .