Równanie kwadratowe z wartością bezwzględną Kuba7: Witam ! Mam problem z jednym równaniem. Równanie jest następujące: |x² − 4| + |x² + 1| = 4x + 1

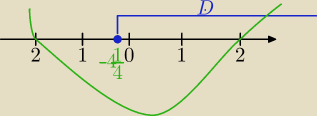
zombi: Po pierwsze wyrażenie pod drugą wartością bezwzględną jest zawsze dodatnie, wobec czego można spokojnie moduł opuścić. Co do pierwszej wartości bezwzględnej, wystarczy zadać sobie pytanie dla jakich "x" wyrażenie x²−4 jest dodatnie, a dla jakich ujemne. Następnie opuszczamy moduł z plusem albo minusem w zależności od tego w którym przedziale się aktualnie znajdujemy. Próbuj, jak będziesz miał więcej pytań to pisz.

Eta: Odp: x=1 v x= √3+1

Mila:

	1
|x2−4|+x2+1=4x+1 , 4x+1≥0,x≥−
	4

|x²−4|+x²=4x x²−4=(x−2)*(x+2) X²−4≥0 dla x≤−2 lub x≥2 1)

	1
x∊<−		,0)
	4

−x²+4+x²=−4x x=−1∉D 2) x∊<0,2) −x²+4+x²=4x x=1 4) x≥2 x²−4+x²=4x 2x²−4x−4=0 rozwiąż