wykaż, że ... Pedro: Wykaż, że równanie x* 2^x = 1 ma rozwiązanie w przedziale ( 0;1)

Jack: Niech f(x) = x*2^x−1 f(0) = − 1 f(1) = 1 Zatem na podstawie tw. Darboux istnieje miejsce zerowe funkcji f(x) w przedziale (0;1), a zatem rownanie ma tam rozwiazanie

Jerzy: To nie jest dobre rozwiazanie Jack .. badasz znak poza dziedziną.

Jerzy: f(1/2) = 1/2*√2 − 1 < 0 f(3/4) = 3/4*1,68 − 1 > 0 i teraz twierdzenie Darboux.

Pedro: Jerzy, skad wziales 1/2 i 3/4?

Pedro: Jack, dzieki! zapomnialem o tw. Darboux ... tylko teraz Jerzy mi namieszal

Jerzy: To dowolne dwie wartości z dziedziny.

Jerzy: Podany przedział jest otwarty , więc pewniejsze jest badanie znaku wewnątrz tego przedziału, a nie na jego końcach.

Pedro: a ok bardzo dziekuje za pomoc

Jack: skoro zbadałem dla wartości krańcowych i wyszło, że one nie są "zerem" no to logiczne, że to w środku musi być?

Adamm: Jerzy, to że tam jest podany taki przedział to nie oznacza że to jest "dziedzina" popatrz sobie co mówi twierdzenie Darboux, i nie pleć bzdur

Eta: x*2^x=1

	1
2x=		, x≠0
	x

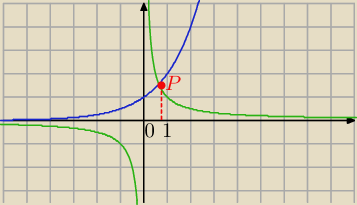
Rysujemy wykresy: y=2^x

	1
y=
	x

P punkt wspólny wykresów x∊(0,1)