Geometria analityczna Asia: Punkt A = (3,4) jest wierzchołkiem trójkąta prostokątnego ABC , o kącie prostym ACB , a S = (0,3) jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że C należy do ujemnej części osi Ox . Udało mi się znaleźć rozwiązanie na innym serwisie, jednak postawiony został tam warunek, że C = (x;0). Skąd wiadomo, że y dla C będzie wynosił 0?

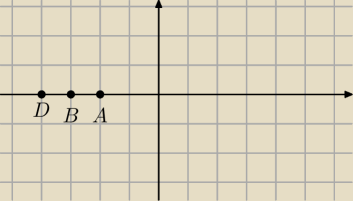
5-latek: Widziisz jakie wspolrzedne maja punkty A B D? wiec jakie wspolrzdne bedzie mial punkt C?

Asia: Ta podpowiedź w ogóle do mnie nie trafia. Według tego co narysowałeś punkt C faktycznie mógłby być (x;0), jednak nie widzę tutaj żadnego związku z zadaniem

5-latek: Ja zadania nie rozwiazywalem Pokazalem Ci tylko dlaczego wspolrzedna y_kowa punktu C=0 (o to pytalas

Asia: Hmm, to chyba nadal nie rozumiem, dlaczego = 0. Nie wiem, co wynika z tego rysunku

5-latek: punkt A=(−2,0) punkt B=(−3,0) punkt D= (−4,0) Jesli punkt C na lezec na osi OX z lewej strony to jakie bedzie mial wspolrzedne ? Ogolnie ?

Asia: Aaa już wiem, nie pomyślałam, że "należy" to dosłownie należy :s dziękuję bardzo <3

Adamm: leży na osi OX więc C=(x; 0) na ujemnej części, więc x<0

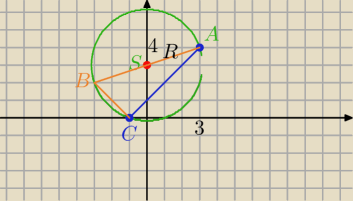
Mila: S=(0,3) − środek okręgu opisanego na Δ prostokątnym, jest środkiem przeciwprostokątnej |SA|=R R=√3²+1²=√10 Równanie okręgu: x²+(y−3)²=√10² C=(x,0) i x<0 x²+9=10 x²=1 x=1∉D lub x=−1 C=(−1,0) B jest punktem symetrycznym do pkt A Względem punktu S⇔S jest środkiem odcinka AB A = (3,4)

	3+xB		4+yB
0=		i 3=
	2		2

B=(−3,2)