Geometria analityczna Ukosnik: W trójkącie równobocznym ABC dane są wierzchołek A = (7,3√3) i środek okręgu wpisanego S = (4,2√3) . Oblicz pole trójkąta ABC. Najpierw obliczyłem długość AS, która wynosi 2√3 , a następnie stosuję wzór na wysokość

	1
okręgu wpisanego w okrąg równoboczny, czyli r =		h.
	3

	2
Jednak z jakiegoś powodu odpowiedź sugeruje, żeby użyć R=		h. Odpowiedź jest błędna, czy
	3

czegoś nie rozumiem?

RadekNieJadek:

	1
promień okręgu wpisanego to odległość od środka okręgu do boku czyli		h
	3

	2
a Tobie potrzebna jest odległość od środka okręgu do wierzchołka trójkąta stąd		h
	3

Ukosnik: Ah, rzeczywiście, dzięki

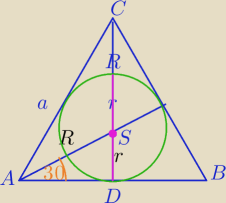Mila: |AS|=R |AS|=√(7−4)²+(3√3−2√3)²=√9+3=√12=2√3 R=2√3, r=√3 1) I sposób |AD|²+r²=R² |AD|²=4*3−3=9 |AD|=3 a=6 ======== 2) II sposób h=|CD| h=3*r=3√3

a√3
	=3√3
2

a=6 ========== 3) ||| sposób W ΔADS:

	|AD|
cos(30o)=
	R

√3		|AD|
	=
2		2√3

|AD|=3 a=6 ==========