Rozwiązanie trójkąta ABC, przypadki
JustOneSimpleQuestion: Rozwiąż trójkąt ABC o boku a=4, b=2+2
√3 oraz kącie γ=30 stopni przy wierzchołku C.
Moje obliczenia i rozwiązania:
c
2=8 (z twierdzenia cosinusów mi tak wyszło)
c=2
√2
| 4 | | 2√2 | |
| = |
| (z twierdzenia sinusów) |
| sin α | | sin γ | |
sin α =
√22
α = 45 stopni lub α = 135 stopni
Nie wiem czy dobrze do tego momentu doszedłem i czy któryś przypadek nie spełnia warunków i czy
jakieś warunki tu istnieją.
19 wrz 18:15
Jack:
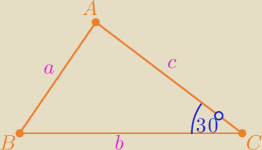
Jedna z mozliwosci:
a
2 = b
2 + c
2 − 2bc * cos30
| | √3 | |
a2 − b2 = c2 − 2bc * |
| |
| | 2 | |
4
2 − (2+2
√3)
2 = c
2 −
√3c * (2+2
√3)
16 − (4+8
√3+12) = c
2 − c(6+2
√3)
−8
√3 = c
2 − c(6+2
√3)
c
2 − c(6+2
√3) + 8
√3 = 0
oczywiscie istnieja miejsca zerowe, ale dosyc nietypowe wiec nie pisze dalej.
19 wrz 19:25
Jack:
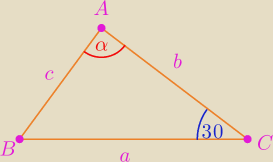
oczywiscie biorac taki przypadek (trojkat) pod uwage (patrz rysunek)
no to :
c
2 = a
2 + b
2 − 2ab cos30
| | √3 | |
c2 = 16 + (2+2√3)2 − 2*4*(2+2√3)* |
| |
| | 2 | |
c
2 = 16 + (16+8
√3) − 4
√3(2+2
√3)
c
2 = 32 + 8
√3 − 8
√3 − 24
c
2 = 8
c = 2
√2 (tak jak mowisz)
2 = 2
√2sinα
| | 1 | |
sinα = |
| −−> α = 45 lub α = 135 |
| | √2 | |
i wtedy do tego miejsca masz ok.
19 wrz 19:35
Jack:
Jeślibyśmy jednak zrobili zamiast tw. sinusów,ponownie tw. cosinusów, to wówczas otrzymamy
| | 1 | |
cos α = |
| zatem tylko α = 45o wówczas pasuje. |
| | √2 | |
tw. sin. daje 2 wyniki, tw. cos daje 1
co jest nie tak?
19 wrz 20:02
Stach:
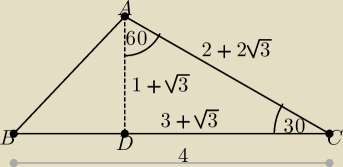
Sprzeczność, bo tu wychodzi, że |BD| < 0, rysunek powinien inaczej wyglądać
19 wrz 20:02
Stach:
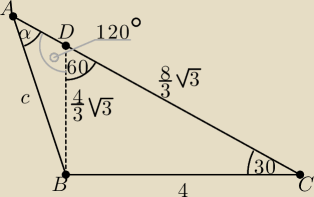
chyba tak
|AC| = 2 + 2
√3
| | 8 | | 2 | |
|AD| = 2 + 2√3 − |
| √3 = 2 − |
| √3 |
| | 3 | | 3 | |
19 wrz 20:03
Jack:
Dokładnie to co napisał Stach,
po narysowaniu i obliczeniu długości boków − wychodzi ujemny bok.
Dlatego tylko kąt α = 45o jest poprawny.
19 wrz 20:04
gg:
20 lut 22:45