Boki trójkąta ABC mają długość: AB=4 , AC=BC=8
a) Obliczyc długości promieni okręgów wpisanego w trójkąt ABC i opisanego na nim.
* to zrobiłam
r=25 √15
R = 1615 √15
b) Oblicz stosunek pól figur na które symetralna boku |AC| przecina ΔABC
Nie wiem co z tym dalej zrobić.
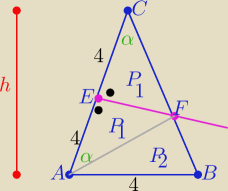h=√82−22= 2√15
| 1 | √15 | |||
P=P(ABC)=......=4√15 i P= | *8*8*sinα ⇒ sinα= | |||
| 2 | 8 |
| 7 | ||
to cosα=√1−sin2α =.......= | ||
| 8 |
| 4 | 32 | |||
zatem |CF|= | = ....= | |||
| cosα | 7 |
| 1 | 32 | 8√15 | ||||
więc P1= | *4* | *sinα=.......... = | ||||
| 2 | 7 | 7 |
| 20√15 | ||
P(ABEF)=P−P1= .... = | ||
| 7 |
| P1 | 2 | |||
to | = ............ = | |||
| P(ABEF) | 5 |