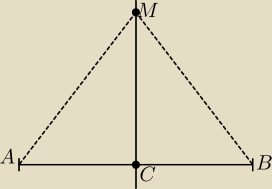
Dowod Powracający: Udowodnuj ze symetralna odcinka niezerowego jest zbiorem wszystkich punktow rowno oddalonych od koncow tego odcinka Zalozenie MA=MB Teza Punkt M lezy na symetralnej odcinka AB Dowod Laczac punkt M z z punktami AB otrzymujemy trojkat rownoramienny Jesli w tym trojkacie punkt M polaczymy ze srodkiem C odcinka AB otrzymamy odcinek MC ktory jest prostopadly do odcinka AB Wiec zgodnie z okresleniem prosta przechodzace przez srodek odcinka i prostopadla do nie go jest symetralna tego odcinka punkt M lezy na symetralnej tego odcinka

Adamm: MC jest prostopadły do AB − dlaczego jeszcze dowód w drugą stronę

Powracający: Zalozenie AC=BC i MC⊥AB Teza MA=MB Dowod ΔAMC≡BMC na zasadzie cechy BKB AC=BC z zalozenia ∡ACM=∡BCM= 90^o CM wspolny dla obu Z tych rownosci wynika ze MA=MB Czy mam Adamm udowodnic ze dwusieczna kata przy wierzcholku w trojkacie rownoramiennym dzieli podsatwe na polowy i jest prostopadla do podstawy?

Adamm: nie sądzę żebyś musiał to udowadniać, ale gdybyś napisał to w dowodzie to myślę że by było w porządku

Powracający: OK