przystawanie walec: Zad 1: W trójkątach ABC i A'B'C' poprowadzono środkoweBD i B'D'. Wykaż że jeśli |BC|=|B'D'| , |BC|=|B'C'| oraz |kąt DBC|=|kąt D'B'C'| to trójkąt ABC = trójkąt A'B'C' Czy wystarczy że pokaże ze trojkat bdc przystaje do d'b'c' i ze trojkat a'd'b' przystaje do abd ? wtedy bedzie pokazane ze trojkaty abc sa takie same po prostu czy musze pokazywac ze abc przytsaje do a'b'c' na jakiejs zasadzie ?

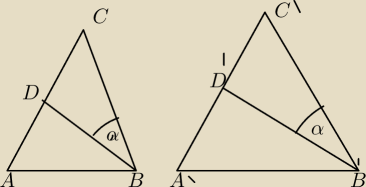
Powracający: Wedlug mnie najpierw nalezy wykazac ze ΔABD≡ΔA'B'C' i wykazac rownosc bokow AB= A'B'

Powracający: ΔABD≡A'B'D' oczywiscie

walec: wykazalem to ze sa przystajace no i wtedy jest ab=a'b' , z zadania mamy cb=c'b' i kąt w B tez jest wiec zasada bkb, ja wszystko rozumiem xD ale chodzi mi o to czy jak pokaze ze oba z tych trojkatow sa przystajace do tych odpowiednich z drugiego rysunku to wystarczy, czy jednak musze napisac stricte ze abc przys do a'b'c' z zasady jakiejs tam

Powracający: Trzeba napisac na podstawie jakiej cechy przystawania trojkatow Tutaj np BKB

walec: ok dzieki