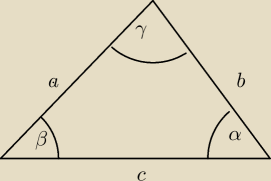
Trojkat i katy > < Powracający: Zadanie a) Udowodnij ze jesli w trojkacie dwa boki sa roznej dlugosci to naprzeciko dluzszego boku lezy wiekszy kąt b) udowodnij ze jesli w trojkacie dwa kąty nie sa rowne to naprzeciwko wiekszego kąta lezy dluzszy bok a) zakladam ze a>b To α>β dalej nie mam pomyslu

master:

a		b
	=		=2R
sinα		sinβ

I szybkie wnioski, jeżeli a>b to sinα> sinβ zatem α>β jezeli α>β to sinα>sinβ zatem a>b

Powracający: dzieki master Zadanie jest w dziale trojkatow przystajacych . Nie mam pojecia jak to wykorzystac tzn te trojkaty

Eta: Dział nie jest ważny ! Na maturze nie napiszą z jakiego działu jest zadanie

Powracający: Oczywiscie Eta ze nie napisza Jesli bedziesz tak miła i napiszesz mi to rozwiazanie z tymi trojkatami to bede wdzieczny

Powracający: Albo po Opolu naprowadzisz

Jack: a) to sie udowadnia z tw. sinusow

	a		b		b sinα
wiemy, ze		=		−−> a =
	sinα		sinβ		sinβ

zalozmy ze wiekszym bokiem jest a. zatem mamy a > b

b sinα
	> b / :b [dzielimy przez b jako, że b > 0 (bo jest bokiem)]
sinβ

sin α
	> 1
sinβ

sin α > sin β zatem α > β

Jack: ahh, juz dawno master to napisal, no coz, nie potrzebnie to otwieram na 30min przed pisaniem odp. , hehe

Powracający:

Jack: http://www.wiw.pl/matematyka/geometria/geometria_02_03.asp

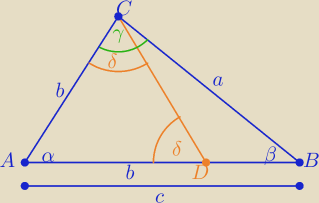
Eta: Jeżeli c>b to γ>β dowód c>b to można zbudować trójkąt równoramienny ADC wewnątrz trójkąta ABC ( punkt D∊AB) kąt γ>δ i kąt δ>β ( bo jest kątem zewnętrznym w ΔDBC zatem γ>β c.n.w

Jack: tam cos powinienes znalezc.

Powracający: Dzieki Eta i Jack

Powracający: b) W trojkacie naprzecie wiekszego kata lezy wiekszy bok Zakladam ze ∡γ>∡β Teza AB>AC Dowod Zalozmy ze AB<AC mamy wtedy albo AB=AC lub AB<AC jesli AB=AC to trojkat ABC bylby trojkatem rownoramiennym i wtedy ∡γ=∡β sprzeczne z zalozeniem jesli AB<AC to ∡γ<∡β ale wczesniej zesmy udowodnili ze ∡γ>∡β czyli znowu sprzecznosc Zatem przyjmujemy ze AB>AC Teza zostala udowodniona