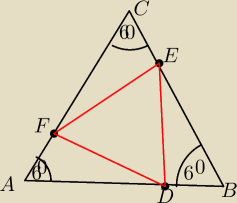
Przystawanie trojkatow Powracający: na bokach AB BC i AC trojkata rownobocznego ABC wybieramy odpowiednio punkty D E i F tak ze AD= BE= CF Udowodnij ze trojkat DEF jest rownoboczny jesli udowodnimy ze ΔAFD≡DBE≡CEF to udowdnimy ze ΔEFD to Δ rownoboczny Z zalozenia AD= BE= CF Z faktu zΔABC rownoboczny to AF= DB=CE oraz z tego samego faktu ∡FAD=∡DBE=∡CEF=60^o Na podstawie cechy BKB ΔAFD≡ΔDBE≡ΔECF Z rownosci tych wynika ze FD = DE= EF to oznacza ze ΔDEF jest rownoboczny

Janek191:

Powracający: dzieki .

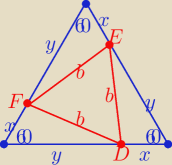Eta: i z cechy(bkb) przystawanie ............

Powracający: Eta dzieki

Eta: Na maturze "czas droższy od pieniędzy"

Powracający: tak masz racje

Eta: Trenuj dalej ..... ( powodzenia