Geometria Doris: Boki trójkąta mają długość: 16 cm, 10 cm, 10 cm. Oblicz odległość między środkiem okręgu wpisanego w ten trójkąt a środkiem okręgu opisanego na tym trójkącie.

Kacper: Najpierw rysunek

5-latek: Czesc A Ty dalej swoje Kacper masz prace ? Pytam bo pisza ze duzo nauczycieli stracilo prace po reformie

Doris: Czy mógłby mi ktoś wyjaśnić jak zrobić to zadanie?

5-latek: Za chwile wyjasnie

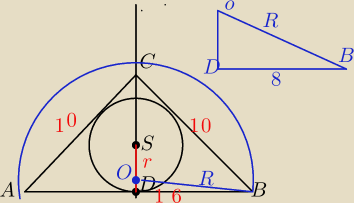5-latek: Kluczowa infornacja dla nas jest taka ze to jest trojkat rownoramienny Wiec po zrobieniu rysunku widzimy ze srodek okregu wpisanego i srodek okregu opisanego na tym trojkacie beda lezec na wysokosci opuszczonej z wierzcholka na podstawe r= SD prpmiem okregu wpisanego w ten trojkat P= p*r P− pole trojkata (chyba najpredziej Heron p− polowa obwodu mam niedokladny rysunek i ten promien okregu opisanego troche mi nie wyszedl Zauwaz z eodleglosc BO to promirn tego okregu

	a*b*c
R=
	4P

POle trojkata juz masz (reszta to kalkulator Wiec OD to bedzie odleglosc srodka okrego opisanego (O) od podstawy R policzysz DB=8 OD z PItagorasa Masz policzyc SO to juz zrobisz .

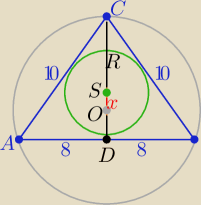Eta: |CD|=h, |CO|=R , |SD|=r |OS|=x −−− szukana odległość x= R+r−h i teraz h=√10²−8²= 6 , P(ABC)= 8*6=48 i P(ABC)=r*(10+10+16)/2

	8
to r=
	3

	a*b*c
R=		⇒ .... R=......
	4P

zatem x= R+r− 6=...... = 5

Mila: Tw. Eulera (geometria) d²=R*(R−2r)

Eta: x²=R²−2Rr