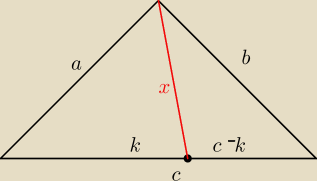
Trojkat odcinek Powracający: Takie zadanie Niech x oznacza dlugosc dowolnego odcinka ktorego jednym koncem jest wierzcholek trojkata a drugim punkt lezacy na boku naprzeciw tego wierzcholka Udowodnij ze

	a+b−c
x>
	2

x+k≥a x+(c−k)≥b 2x+c>a+b 2x>a+b−c

	a+b−c
x>
	2

wiec udowodnione Pyta tez autor zbioru kiedy moze wystapic rownosc i ile razy w tych dwoch poczatkowych nierownosciach slabych ?

Powracający:

Adamm: dowód zły

Powracający: Dlaczego zły?

Adamm: co jeśli 0<k<c ? a co gdy k=0 lub k=c ? rozpatrz 2 przypadki a z x+k≥a oraz x+(c−k)≥b nie wynika wcale że 2x+c>a+b

Powracający: Mam taka sama odpowiedz w zbiorze Adamm Autor tez pisze te dwie nierownosci slabe i z tego ze rownosc moze zachodzic co najwyzej raz (wlasnie pyta kiedy? przy dodawaniu stronami piszsemy nierownosc ostra czyli rownosc zachodzi kiedy k=0 lub k=c ? Jesli 0<k<c to juz rozpisalem Drugi przypadek szczerze powiem nie wiem .

Adamm: wtedy też równość nie zachodzi jak k=0 to x=a jak k=c to x=b

	a+b−c
jak przekształcisz równoważnie x=		, to wyjdzie ci że a+b=c lub podobne
	2

czyli ten trójkąt musiał by być odcinkiem

Powracający: OK. dobrze .

Powracający: To bylo ostanie zadanie z tego dzialu oprocz zadan konstrukcyjnych ktorym potem poswiece wiecej czasu dzieki za pomoc