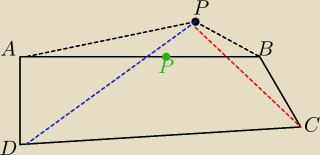
Punkt na plaszczyznie i czworokąt Powracający: Zadanie Wykaz ze suma odleglosci dowolnego punktu plaszczyzny od wierzcholkow dowlnego czworokata wypuklego jest wieksza od polowy jego obwodu PA+PB≥AB PB+PC≥BC PC+PD≥CD PD+PA≥AD 2(PA+PB+PC+PD)>AB+BC+CD+AD

	AB+BC+CD+AD
PA+PB+PC+PD>
	2

Mam pytanie czy dlatego tutaj piszemy najpierw nierownosci slabe bo nie wiemy tak naprawde gdzie ten punkt P lezy ? No bo np gdy bedzie jednym z wierzcholkow to rownosc wystapi w dwoch nierownosciach np jesli bedzie wierzcholkiem A to bedzie PA+PB=AB i PA=0 PA+PD=AD i PA=0? Jeszcze wedlug mnie bedzie jedna rownosc z tych czterech nierownosci gdy punkt P bedzie lezal np na bolu AB zanaczylem go na zielono wtedy bedzie AP+PB=AB

Powracający:

Adamm: tutaj też wystarczy rozpatrzeć 1. P nie leży na wierzchołku 2. P leży na wierzchołku

Adamm: albo na boku, jeszcze może być taka opcja

Powracający: To rozumiem Wiec dlatego przy dodawaniu stronami piszemy nierownosc ostra?

Adamm: jak masz same nierówności słabe, to w wyniku dostaniesz nierówność słabą ale my chcemy ostrą możesz też napisać te nierówności słabe, i sprawdzić czy może być PA+PB=AB itd. jednocześnie jeśli nie, to równość nie może zajść, i i tak nierówność będzie ostra