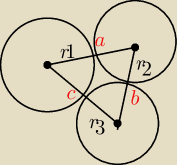
Okregi -promienie Powracający: Srodki trzech okregow parami zewnetrznie stycznych sa wierzcholkami trojkata o bokach dlugosci a b c Oblicz promienie tych okregow r₁+r₂= a r₂+r₃= b r₁+r₃= c 2r₁+2r₂+2r₃= 2p −obwod tego trojkata r₁+r−2+r₃=p −− polowa obwodu a+r₃=p r₃= p−a r₁+b=p r₁= p−b c+r₂=p r₂= p−c

Pytający: Twoje założenia są błędne: a+r₃=p zachodzi jedynie, gdy a=b r₁+b=p zachodzi jedynie, gdy b=c c+r₂=p zachodzi jedynie, gdy a=c r₁+r₂= a r₂+r₃= b r₁+r₃= c Z dwóch pierwszych równań:

	a+b−r1−r3
r1+2r2+r3= a+b ⇒ r2=
	2

Z dwóch ostatnich równań:

a+b−r1−r3
	+2r3+r1= b+c ⇒ a+b−r1−r3+4r3+2r1=2b+2c ⇒ r1=b+2c−a−3r3
2

Z trzeciego równania:

	−a+b+c
(b+2c−a−3r3)+r3= c ⇒ r3=
	2

	−a+b+c		a−b+c
r1=b+2c−a−3r3=b+2c−a−3*		=
	2		2

	a+b−r1−r3		a−b+c   −a+b+c   a+b− −   2   2		a+b−c
r2=		=		=
	2		2		2

kochanus_niepospolitus: a nie prościej tak: (1) r₁ + r₂ = a −> r₁ = a − r₂ (2) r₂ + r₃ = b −> r₂ = b − r₃ podstawiamy do (1) i mamy: r₁ = a − b + r₃ (3) r₃ + r₁ = c −> r₃ = c − r₁ podstawiamy dalej do tego co mieliśmy i mamy: r₁ = a − b + c − r₁ −> 2r₁ = a − b + c −> r₁

	a−b+c
=
	2

natomiast podstawiając r₁ = c − r₃ otrzymamy:

	−a+b+c
−a+b+c = 2r3 −> r3 =
	2

r₂ bez problemu wtedy wyliczymy z pierwotnej postaci (1) bądź (2)

Powracający: Pytajacy Nie wiem dlaczego bledne Moje rozwiazanie pokrywa sie z odpowiedzia ze zbioru zadan z ktorego korzystam Oczywiscie przeanalizuje Twoje i kochanusa rozwiazania .

Pytający: Kochanus, ano prościej. Powracający, coś mnie się pomieszało − tamte założenia są dobre. Wszystko tam masz dobrze (tylko nie doszedłeś do odpowiedzi z użyciem wyłącznie boków a, b, c).

Powracający: dziekuje Ci