Granica ciągu amm: W prostokąt wpisano k_n okręgów o jednakowych promieniach. Niech a i b oznaczają długości

	a
boków prostokąta, a		promień wpisanych okręgów. Znaleźć granicę stosunku Skn/S przy
	2n

n→∞, jeżeli Sk_n oznacza pole k_n wpisanych okręgów, a S pole danego prostokąta

	a
rk=
	2n

	a2
Skn=π*		*n*... ?
	4n2

jakaś pomoc?

Tadeusz: Czy to jest dokładnie przepisana treść zadania? ... czy też troszkę własnymi słowy

amm: dokładnie przepisane

amm: https://zapodaj.net/669f47143f35c.jpg.html

Pytający: Pola okręgów... ciekawe zadanie.

	a
r=
	2n

	a
2r=		// średnica
	n

Zatem w prostokącie o bokach a i b mamy wpisanych:

	a		b		ab		bn2
kn=		*		=		=		okręgów.
	2r		2r		a   ( )2   n		a

S_kn − niech jednak oznacza pole tych wpisanych kół, nie okręgów

Skn		bn2   a   *π*( )2 a   2n		π
	=		=
S		ab		4

Zatem:

	Skn		π
limn→∞		=
	S		4

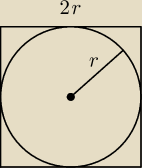kochanus_niepospolitus: Zadanie to można było o wiele łatwiej rozwiązać Wystarczy zauważyć, że bez różnicy jak mały promień okręgu będzie, to i tak będziemy mieli stałą wartość

Po		πr2		π
	=		=		<−−− taką część jeden okrąg zajmuje w kwadracie o boku
P□		4r2		4

'2r'

	Skn		π		b   *n2 a		π
limn−>∞		=		*		=
	S		4		b   *n2 a		4