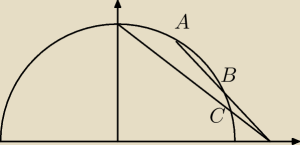
 Na rysunku widzimy półokrąg o promieniu 1 i dwie proste przecinające półokrąg
w punktach A, B, C (resztę widać na rysunku).
Znamy współrzędne poziome A i B (niech to będą liczby a,b). Należy znaleźć współrzędną
poziomą c punktu C.
Na rysunku widzimy półokrąg o promieniu 1 i dwie proste przecinające półokrąg
w punktach A, B, C (resztę widać na rysunku).
Znamy współrzędne poziome A i B (niech to będą liczby a,b). Należy znaleźć współrzędną
poziomą c punktu C.
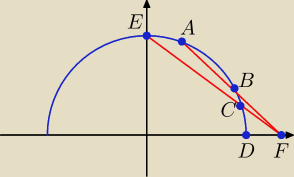 1. równanie okręgu x2 + y2 = 1, y ≥ 0, y = √ 1 − x2 ,
2. A = (a, √ 1 − a2 ), B = (b, √ 1 = b2 ),
3. równanie prostej AB, jej miejsce zerowe x0, F = (x0, 0),
4. równanie prostej EF, E = (0, 1),
5. Z układu równań: x2 + y2 = 1 i równanie prostej EF wyznaczymy C
1. równanie okręgu x2 + y2 = 1, y ≥ 0, y = √ 1 − x2 ,
2. A = (a, √ 1 − a2 ), B = (b, √ 1 = b2 ),
3. równanie prostej AB, jej miejsce zerowe x0, F = (x0, 0),
4. równanie prostej EF, E = (0, 1),
5. Z układu równań: x2 + y2 = 1 i równanie prostej EF wyznaczymy C
| AF*BF | ||
CF= | ||
| EF |
| −2abx | |
+b+a=c | |
| x2+1 |
| a−b | a−b | ||
x+a− | √1−a2=0 | ||
| √1−a2−√1−b2 | √1−a2−√1−b2 |
| 1+ab+√1−a2√1−b2 | ||
x= | ||
| √1−a2+√1−b2 |