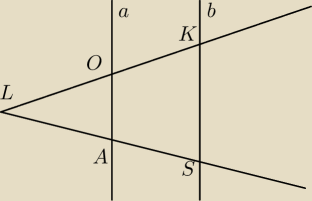
Twierdzenie talesa - Proste a i b przecinają ramiona kąta o wierzchołku L Przemek34: Proste a i b przecinają ramiona kąta o wierzchołku l tak ze na jednym ramieniu powstaly odcinki LO i OK, a na drugim LA i AS. Punkty A i O leżą bliżej punktu L niż punkty S i K. Sprawdz czy proste a i b są równoległe, korzystając z podanych informacji : a)|LO| : |LK|=2:3 , |LA|=4 , |AS|=6 b) |LO|=2 , |OK| = 3 , |OA|=6 , |KS|=15 c)|LO| : |LK|=1:8 , |OA|=2 , |KS|=16 d)|LO|= 1 i 1/4 , |OK|=2 i 1/2 , |LA|=|OK|−0,3 , |LS| = |LA| + 2,2 odpowiedzi do zadań = b), c) − tak, a) d) − nie Proszę o obliczenia potrzebuję pilnie na jutro !

kochanus_niepospolitus: a chociaż rysunek zrobiłeś

kochanus_niepospolitus: z tw. Talesa: a)

LO		LA
	=
LK		LS

b)

LO		OA
	=
LK		KS

c)

LO		OA
	=
LK		KS

d)

LO		LA
	=
LK		LS

jeżeli te proporcje są zachowane to dla danego podpunktu proste a i b są równoległe, w przeciwnym razie nie są

Przemek34: Nie mam rysunku bo jest to obecnie dla mnie ciemna magia nie było mnie w szkole od początku roku jutro wracam a mam to obowiązkowo mieć zrobione, dopiero jutro na dodatkowych lekcjach się tego nauczę dlatego proszę o pomoc.