sinusy damian_błaszczak: Dany jest trójkąt równoboczny ABC. Niech E i F to środki odpowiednio boków CA, AB. Niech bedzie dany punkt P należący do okregu opisanego na tym trójkacie tak że CP jest prostoapadłe do EF. Oblicz sin²(∡EFP)+sin²(∡EPF)

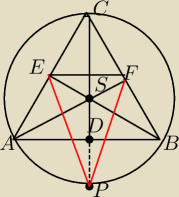
Powracający: W trojkacie rownobocznym wysokoc jest jednoczesnie srodkowa i dwusieczna kata

	2
Cs=		CD
	3

Widzisz gdzie musi lezec P zeby CP ⊥EF bylo?

kochanus_niepospolitus: Powracający ... fajnie tylko F leży na AB, a nie BC

kochanus_niepospolitus:

	x
y =
	2

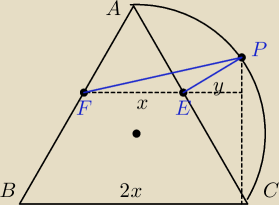
więc rysunek będzie tak wyglądał

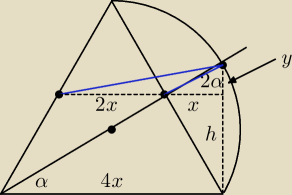
kochanus_niepospolitus: α = 30^o 2α = 60^o

	x		√3
tg60o =		−> y =		x
	y		3

	2√3
EP = √1/3 + 1x =		x
	3

	28√3
PF = √1/3 + 9x =		x
	3

z tw. cosinusów: EP² = PF² + EF² − 2|EF|*|PF|*cos(∡EFP) −> stąd cos(∡EFP) analogicznie cos(∡EPF) wyliczasz sin²(∡EFP) + sin²(∡EPF) = 2 − (cos²(∡EFP) + cos²(∡EPF))

Powracający: No tak. Zle przeczytalem . Przepraszam .

Powracający: Pomozesz w moim?

kot: Jak jest tu odpowiedź chętnie sie z tym sprawdzę

kochanus_niepospolitus: Ja pokazałem kolejne kroki jak wyliczyć tą wartość ... pozostaje wyznaczyć tylko wartości tychże cosinusów (szczerze mówiąc nie chce mi się tego robić)

kochanus_niepospolitus: Najistotniejsze było zauważenie, że BP zawiera w sobie punkt E (co jest konsekwencją tego, że mamy tutaj trójkąt równoboczny)

damian_błaszczak: wyszło mi 1/7 dobrze?