Szeregi Incr0: Witam, mam problem z zadaniem i nie wiem jak się do niego zabrać. Przeglądałem notatki ale nigdzie nie mogę znaleźć podobnego przykładu. Dla jakich wartości "a" szereg ∑ (4a² + 6a + 1)ⁿ jest zbieżny? Oblicz jego wartość dla a =

	1
−
	4

Proszę o wyjaśnienie, pozdrawiam

kochanus_niepospolitus: Szereg: ∑ bⁿ będzie zbieżny ⇔ |b| < 1 stąd masz: |4a² + 6a+1| < 1 <−−− rozwiązujesz Pamiętasz może ciągi geometryczne w liceum? miałeś tam: a₁ , a₁*q, a₁*q², .... suma tego ciągu (czyli nic innego jak a₁*∑qⁿ⁻¹) będzie istniała (czyli szereg będzie zbieżny) tylko wtedy, gdy |q| < 1

Incr0: Wielkie dzięki, z tym równaniem bez problemu sobie poradzę. Rozumiem, że wynik, który mi wyjdzie będzie przedziałem tego "a", w którym jest zbieżność.

kochanus_niepospolitus: dokładnie tak

kochanus_niepospolitus: ten szereg to nic innego jak suma nieskończonego ciągu geometrycznego gdzie a₁ = q = (4a²+6a+1)

Incr0: Tak już w ramach sprawdzenia, wychodzi tutaj przedział (−³₂ ; 0)? I czy n=0 pod znakiem ∑ wpływa na wynik?

kochanus_niepospolitus: oczywiście, że wpływa: ∑_n=0 bⁿ = 1 + ∑_n=1 bⁿ ... ponieważ:b⁰ = 1 (dla dowolnego b∊R)

kochanus_niepospolitus: tzn. wpływa na samą wartość sumy (szeregu), ale nie wpływa na to czy dany szereg jest zbieżny czy też nie.

kochanus_niepospolitus: źle wyliczony przedział

kochanus_niepospolitus: niech a = −0.75

	9		9
4a2 + 6a + 1 = 4*		− 2		+ 1 > 1
	16		16

Incr0: Ok, rozumiem. Jeśli chodzi o dalszą część zadania: Oblicz jego wartość dla a = −¹₄. Podstawiam za a podaną wartość ale dalej zostaje mi "n".

kochanus_niepospolitus:

	9		9		9
tfu ... 4*		− 8*		+ 1 = − 4*		+ 1 < −1
	16		16		16

Incr0: aaa po prostu, ok dzięki

kochanus_niepospolitus: ponownie wylicz prawidłowy przedział, kiedy ten szereg jest zbieżny

Incr0: −1<4a² +6a+1<1 rozłożyłem na: 4a²+6a+2>0 oraz 4a²+6a<0 a= −1 a=−³₂ a= −¹₂ a = 0 Wnioskowałem, że skoro mniejszy zbiór zawiera się w większym to większy jest odpowiedzią.

kochanus_niepospolitus: zauważ, że: z (I) wychodzi a∊(−∞,−1) u (−0.5, +∞) z (II) wychodzi a∊(−3/2 , 0) więc część wspólna to Jaki błąd popełniłeś NIE ZROBIŁEŚ SZKICU PARABOL

Incr0: czyli wyjdzie na ten mniejszy (−1; −0,5)

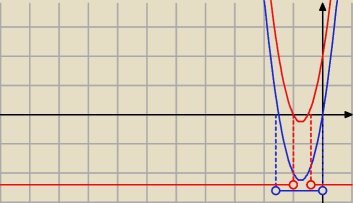
kochanus_niepospolitus: NIIIIEEE. Jaka jest CZĘŚĆ wspólna tych rozwiązań zauważ, że pierwsza parabola ma być >0 a druga <0

Incr0: (−3/2;−1) u (−0,5;0)

kochanus_niepospolitus: tak

Incr0: Dzięki, już mi się wszystko pomieszało z nerwów ale teraz już wiem o co chodzi.