zadanka Metis: Przy pomocy tw. Gaussa oblicz strumień pola F = [x³,y³,z³] przepływający przez obszar zamknięty powierzchniami z = √ x² + y² , z = 3 Potrzebuję pomocy

Adamm: dobrze przepisałeś treść?

Metis: Jasne, F = [x³,y³,z²], mój błąd

Adamm: ten strumień nie ma przypadkiem być po powierzchniach z=√x²+y² oraz z=3 ? i czy po zewnętrznej, czy wewnętrznej stronie

Metis: W zad. mam przez ale to może być błąd.

Adamm: dobra, nieważne x=rcosθ y=rsinθ div. F = 3(x²+y²+z²)=3(r²+z²) ∫₀^2π ∫₀³ ∫_r³3r(r²+z²) dz dr dθ = ...

Metis: Dzięki całkę już sobie policzę. Mam jeszcze kilka , pomozesz mi?

Adamm: oczywiście

Metis: Obl. masę pierścienia wyciętego z paraboloidy z = x² + y² przez płaszczyzny z = 1; z = 4 o gest. pow. δ = z

Metis: Dzięki

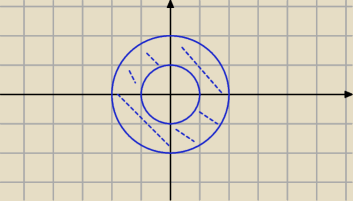
Adamm: x=rcosθ y=rsinθ δ=r² r∊<1;2>, θ∊<0;2π> ∫∫_Dz√x'²+y'²+1dA = ∫₀^2π ∫₁² r*r²*√4r²+1 dr dθ = ...

Adamm: nie wiem czemu ale napisałem tam √x'²+y'²+1 powinno być √z_x²+z_y²+1

Metis: Ok Przy pomocy tw. Greena obliczyć: ∮ xydx + x²dy ¬ gdzie ¬ jest brzegiem obszaru ogr. krzywymi x = y², x = 4

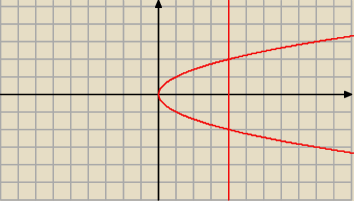
Adamm: y2≤x≤4, −2≤y≤2 całka = ∫−22 ∫y24 x dx dy = ...

Adamm:

	d(x2)		d(xy)
x w całce bo		−		=2x−x=x
	dx		dy

Metis: Jasne Oblicz długość spirali log. o gęstości danej parametrycznie: ¬ = {[e^−t cost; e^−t sint; e^−t]; t ∊ <0, π/2 > }

Adamm: gęstości?

Metis: Dokładnie.

Adamm: rozumiem że trzeba obliczyć długość tej spirali, ale treść jakaś dziwna...

Metis: http://prntscr.com/gkss5m

Adamm: eh, nieważne v=[e^−tcost; e^−tsint; e^−t] v'=[−e^−t(sint+cost);e^−t(cost−sint);−e^−t] |v'|=e^−2t√3 L=∫₀^π/2 √3e^−2t dt = ...

Metis: Ok, gdy nie bede wiedział z czegoś coś wziąłeś to będę jutro pytał. Kolejne: http://prntscr.com/gksy56

Adamm: v=[cost+tsint; sint+tcost] v'=[tcost; 2cost−tsint] |v'|=√4cos²t−4tsintcost+t² ∫₀^π (1+4tsintcost+t²)√4cos²t−4tsintcost+t² dt = ...

Metis: Możesz wyjaśnić mi to zadanie: http://prntscr.com/gkt3az ?

Adamm: wychodzi ten wzór z tw. Green'a v=[2cost+cos2t; 2sint+sin2t] v'=[−2sint−2sin2t; 2cost+2cos2t] |v'|=√8+8sintsin2t+8costcos2t V=∫₀^2π (2cost+cos2t)√8+8sintsin2t+8costcos2t dt = ...

Adamm: ja się tylko zastanawiam jak ty te całki policzysz

Metis: http://prntscr.com/gkt7sp

Metis: Będę musiał

Adamm: x=2cosθ, y=2sinθ

	4cosθ−2sinθ−3
z=
	2

θ∊<0; 2π>

	4cosθ−2sinθ−3
v=[2cosθ; 2sinθ;		]
	2

	−4sinθ−2sinθ−3
v'=[−2sinθ; 2cosθ;		]
	2

|v'|=√16+(4sinθ+2sinθ+3)²/2 P= ∫₀^2π cosθ√16+(4sinθ+2sinθ+3)² dθ = ...

Metis: Dużo liczenia

Adamm: w v', we współrzędnej z

−4sinθ−2cosθ
2

|v'|=√16+(4sinθ+2cosθ)²/2 P= ∫₀^2π 2cosθ√4+(2sinθ+cosθ)² dθ = ...

Metis: Jak bedzie wyglądało podstawienie walcowe? Całkę policzę już sam. http://prntscr.com/gktdj5

Adamm: x=rcosθ, y=rsinθ 0≤r≤sinθ, 6−rcosθ≤z≤18−rcosθ, 0≤θ≤π

	rcosθ
∫0π ∫0sinθ ∫6−rcosθ18−rcosθ		dz dr dθ = ...
	z

Metis: A tutaj ? http://prntscr.com/gkthhl

Adamm: zapomniałem o jakobianie z roztargnienia dopisz go sobie

Adamm:

	2
x2+y2=
	1+x2+y2

(x²+y²)²+(x²+y²)−2=0 x²+y²=1 x=rcosθ, y=rsinθ

	2
r∊<0;1>, θ∊<0;2π>, z∊<r2;		>
	1+r2

∫02π ∫01 ∫r22/(1+r2) r dz dr dθ

Metis: I mam jeszcze takie 3 ostatnie http://prntscr.com/gktqlk

Adamm: 1. r(t)=[cos³t; sin³t] r'(t)=[−3cos²t*sint; 3sin²t*cost] F(r(t))=[−2cos³t; 2sin³t] ∫₀^π/2 F(r(t))•r'(t) dt = ∫₀^π/2 6cos⁵t*sint+6sin⁵t*cost dt = ... 2. r_u=[2u; 0; v] r_v=[0; 2v; u] |r_uxr_v|=√4v⁴+4u⁴+16u²v² P=∫₀¹ ∫_v¹ |r_uxr_v| du dv 3. div. F = 3 x=rcosθ, y=rsinθ r∊<0;2>, θ∊<0;2π> ∫∫∫_V 3 dxdydz = ∫₀^2π ∫₀² ∫₋₁¹ 3r dz dr dθ

Metis: Dzięki wielkie!

Adamm: 23:26 przykład drugi pamiętam że próbowałem rozwiązać już wcześniej nawet wolfram podaje przybliżony wynik

Metis: Dziękuję jeszcze raz Jak czegoś nie będę wiedział to będę pisał.