2 pytania :))
kasia123: 1) Jeśli mam
f(x) = |x|
to
f(−x) = −|x| czy f(−x)=|−x|
2) Czy aby narysować wykres
(−x
2+4x−3)/(x−2) = y
muszę zrobić przebieg zmienności funkcji?
13 wrz 20:23
Adamm: 1. drugie
2. tak
czy jest to część zadania? prawd. można zrobić je inaczej
13 wrz 20:24
kasia123: Muszę rozwiązać graficznie nierówność.
x−1/x−2 > x−1 (lewa strona w ||), rozbiłam na dwa przypadki. Ten w treści pytania to jeden z
nich
13 wrz 20:32
kasia123: chyba, że narysować prostą x−1 i wtedy to co pod nią (wyznaczone przez to w wartości)
zakreślić... czy tak nie wyjdzie?
13 wrz 20:34
Adamm:
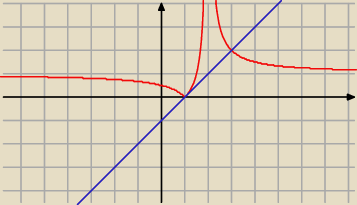
x∊(−
∞;1)∪(1;3)
13 wrz 20:37
Adamm: masz wyznaczyć te x dla których czerwona funkcja jest nad tą niebieską
13 wrz 20:37
5-latek: Lewa strona
wiec
| x−1 | | 1(x−2)+1 | | 1 | |
| = |
| = 1+ |
| |
| x−2 | | x−2 | | x−2 | |
13 wrz 20:44
kasia123: Jeszcze dopytam dla pewności o drugi przykład, dobrze?
mam
−4/(x+4) − 2 <=0
to wyznaczam x, które mają wartość większą lub równą 0, zgadza się? <−6,−4>
13 wrz 20:47
kasia123: które są nad osią OY
13 wrz 20:48
Adamm: założenie: x≠−4
−4(x+4)−2(x+4)2≤0
(x+4)2+2(x+4)≥0
(x+4)(x+6)≥0
x∊(−∞;−6>∪(−4;∞)
jak mnożymy przez coś ujemnego to musimy zmienić znak nierówności
13 wrz 20:50
Adamm:
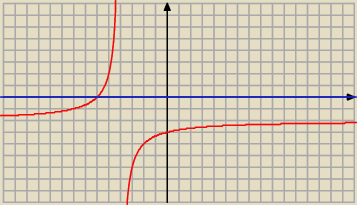
wyznaczamy x dla których czerwona funkcja jest pod niebieską
13 wrz 20:52
kasia123: napisałam pół przykładu, haha... ale tak tak, zgadza się
13 wrz 20:53
kasia123: dziękuję za pomoc!
13 wrz 20:55
kasia123: dziękuję za pomoc!
13 wrz 20:56
kasia123: A gdybym tam nie było <=0, tylko <=y, to zaznaczamy obszar pod czerwonymi wykresami?
13 wrz 20:58
Adamm: nad czerwonymi
13 wrz 21:00
13 wrz 21:09