Optymalizacja Opty: Mam rozwiązań metodą graficzną zadanie z optymalizacji. 2x₂ − 2x₁ → max x₁ − x₂ ≥ 1 0,5 x₁ − x₂ ≥ −1 x_j ≥ 0 , j=1,2

mat: no to rysuj! x₂=x₁ − 1 x₂=0.5x₁+1 (x₂ to jakby y, x₁ to x jak mamy y=ax+b)

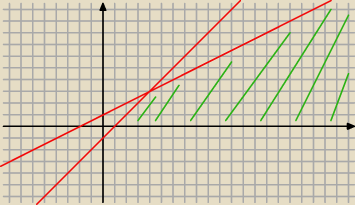
Adamm: f(x₁, x₂)=2x₂−2x₁ musimy mieć jak najwięcej x₂, i jak najmniej x₁ więc maksimum będzie gdzieś albo na prostej x₂=x₁−1 dla x₁∊<1;4> albo na x₂=0,5x₁+1 dla x₁∊<4;∞> f(x₁, x₁−1)=−2 f(x₁, 0,5x₁+1)=−x₁+2 <− największe dla x₁=4 i równe −2 czyli f osiąga swoje maksimum dla x₁∊<0;4>, x₂=x₁−1 które wynosi −2

Adamm: za drugim razem napisałem <0;4>, oczywiście pomyłka i miało być <1;4>

Opty: nie rozumiem tego opisu wyboru maksimum

Adamm: pomyśl sobie tak masz jakieś x₁ (dali ci) i jak wybierzesz x₂ żeby 2x₂−2x₁ było największe? no oczywiście, x₂ musi być jak największe i kropka dlatego właśnie te 2 proste sprawdzamy