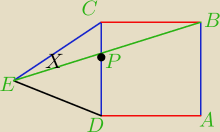
 Dany jest prostokąt ABCD. EC=AB oraz BP= √72 ,EP= 3√2. Oblicz kąt PEC
Dany jest prostokąt ABCD. EC=AB oraz BP= √72 ,EP= 3√2. Oblicz kąt PEC
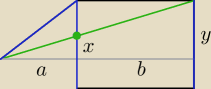 √72 = √9*4*2 = 6√2
z tw. Talesa
√72 = √9*4*2 = 6√2
z tw. Talesa
| a | a+b | a | a+b | ||||
= | ⇔ | = | ⇔ b = 2a | ||||
| 3√2 | 3√2 + 6√2 | 3√2 | 9√2 |
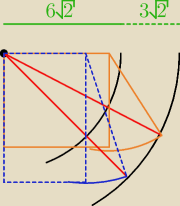 Jak dla mnie to brakuje nam jakiejś jednej danej.
Z tymi danymi zadanie jest nie do rozwiązania.
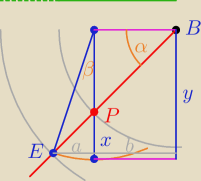
Zarówno niebieski jak i beżowy prostokąt + EC spełniają warunki zadania.
Mała niedokładność (AB i CD powinny być nieznacznie dłużej, tak aby punkt C był punktem
wspólnym prostokąta i łuku) wynika z ograniczeń wynikających z rysowania w edytorze.
Jak dla mnie to brakuje nam jakiejś jednej danej.
Z tymi danymi zadanie jest nie do rozwiązania.
Zarówno niebieski jak i beżowy prostokąt + EC spełniają warunki zadania.
Mała niedokładność (AB i CD powinny być nieznacznie dłużej, tak aby punkt C był punktem
wspólnym prostokąta i łuku) wynika z ograniczeń wynikających z rysowania w edytorze.
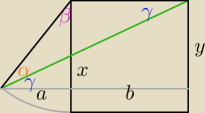 Skoro wykazałem, że takich sytuacji będzie nieskończenie wiele ( o ile x∊(0, 3√2) ) to
spojrzymy na dwa wybrane przypadki i sprawdzimy, czy kąt aby na pewno się będzie różnił:
1) niech x = √2
w takim razie a = √16 = 4
Skoro wykazałem, że takich sytuacji będzie nieskończenie wiele ( o ile x∊(0, 3√2) ) to
spojrzymy na dwa wybrane przypadki i sprawdzimy, czy kąt aby na pewno się będzie różnił:
1) niech x = √2
w takim razie a = √16 = 4
| x | √2 | |||
tg γ = | = | −> γ ≈ 19.47o | ||
| a | 4 |
| a | 4 | 2√2 | ||||
tg β = | = | = | −> β ≈ 43.31o | |||
| y | 3√2 | 3 |
| x | 3 | |||
tg γ = | = | = 1 −> γ ≈ 45o | ||
| a | 3 |
| a | 3 | 1 | ||||
tg β = | = | = | −> β ≈ 18.43o | |||
| y | 9 | 3 |
| BP−EP | ||
kolega mi podał że tyle tgx=( | )1/2 ale nie wiem skąd on to wziął | |
| BP+EP |
 no to rozpiszmy to i zobaczymy do czego dojdziemy:
no to rozpiszmy to i zobaczymy do czego dojdziemy:
| sin2x | BP−EP | ||
= | |||
| cos2x | BP+EP |
| EP | |
= cos(2x) | |
| BP |
| 1 | |
= cos(2x) −> 2x = 60o −> x = 30o | |
| 2 |
| x | 3√2 | ||
= | −> y = 3x | ||
| y | 9√2 |
| y−x | ||
sin45o = | −> x = 3 | |
| 6√2 |
| a | 3√2 | ||
= | −> b = 2a | ||
| a+b | 9√2 |
| a | 3 | 1 | ||||
tg β = | = | = | −> β ≈ 18.43o | |||
| y | 9 | 3 |
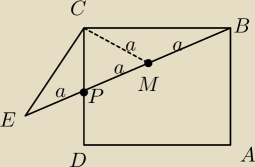
 Niech a=PE=3√2 więc BP=2a. Niech y=AB oraz M środek BP. Trójkąty BMC, PMC są równoramienne z
kątem x= MBC=BCM ,wiec y=2acosx Z twierdzenia kosinusów dla BCE mamy 2y2(1+cos 2x)=9a2.
Niech a=PE=3√2 więc BP=2a. Niech y=AB oraz M środek BP. Trójkąty BMC, PMC są równoramienne z
kątem x= MBC=BCM ,wiec y=2acosx Z twierdzenia kosinusów dla BCE mamy 2y2(1+cos 2x)=9a2.
 a niby dlaczego:
∡x = ∡MBC
a niby dlaczego:
∡x = ∡MBC  dlaczego przyjmujesz, że EC = CB
dlaczego przyjmujesz, że EC = CB  Czyli, że mamy tutaj kwadrat, skoro sam wyraźnie zaznaczyłeś, że mamy prostokąt.
Czyli, że mamy tutaj kwadrat, skoro sam wyraźnie zaznaczyłeś, że mamy prostokąt.