pilna pomoc ! ekstrema sed: w półokrąg o promieniu 1 wpisano prostokąt ABCD, oblicz boki prostokąta tak aby pole było jak największe

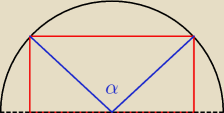
Adamm: P=sinα pole będzie największe dla α=π/2 wtedy boki prostokąta to √2/2 oraz √2

sed: zadanie należy zrobic z pochodnej

Adamm: niczego takiego nie ma w poleceniu

sed: ale taki to dzial nie potrafie ułozyc załozenia zeby zrobic pochodna

Adamm: niech boki to x, y 1>x>0, 1>y>0, x+y>1 y=√1−x² z tw. Pitagorasa P=x√1−x²=√x²−x⁴ g(x)=x²−x⁴ <− liczysz ekstrema dla 1>x>0

Adamm: y=2√1−x² chociaż zupełnie nic to nie zmienia

Adamm: no i 2>y>0, 2x+y>1

sed: ok ale czy połowa podstawy = wysokosci prostokata? nie prawda?

sed: mozesz to dokłądnie policzyc z rozwiązaniem mam kilka obiekcji a potrzebuje to jutro na 7:10 na spr

Adamm: sam sobie to licz

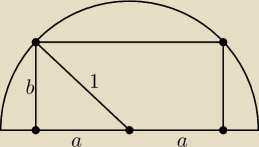
Parys: 0<a<1 i 0<b<1 a² + b² = 1, b = √1 − a² P = 2ab, P = 2a*√1 − a², P = √−4a⁴ + 4a² P jest największe wtedy gdy funkcja f(a) = −4a⁴ + 4a² osiąga maksimum

	√2		√2
f'(a) = −16a3 + 8a = −16a(a −		)(a +		)
	2		2

	√2
maksimum dla a =		, wtedy b = a
	2

sed: Dzięki PArys , Adamm jak masz problem sam ze sobą to idz spac

Adamm: spytałeś się czy ci to policzę to ci odpowiedziałem

sed: ja tak samo liczyłem i 45 minut licze pododną ale z pierwiastiem i tu nie mogło mi wyjść, dlaczego w pochodnej opuszczamy pierwiastek zamiast (....)¹/2 i jazda...