funkcje kasia123: 1) √x²+7 > √2x+3√2 √x⁴−x² <= 4−x² czy mogę podnieść obie strony do kwadratu w tych nierównościach? (kiedy nie można tego robić?) 2) Dla jakich wartości parametru m trójmian kwadratowy y=(m+1)x² + 2x − 4m + 1 ma przynajmniej jeden pierwiastek dodatni? Założenia itd. rozumiem do funkcji kwadratowej. Jednak nie rozumiem dlaczego w tym zadaniu nie sprawdzamy przypadku funkcji liniowej? Czy funkcja liniowa nie ma "pierwiastka", kiedy y=0?

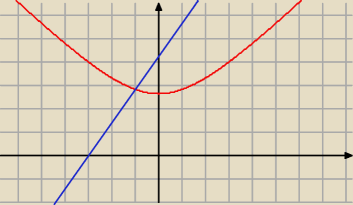
Janek191: 1) √x² +7 > √2 x + 3√2 Można dla x > − 3

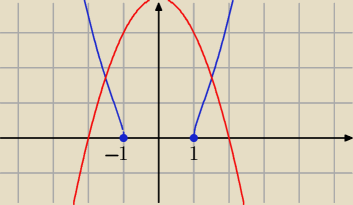
Janek191: 1) √x⁴ − x² ≥ 0 dla dowolnego x ∊ ℛ \ ( − 1, 1) √x⁴ − x² ≤ 4 − x²

kasia123: A jak rozwiązać bez podnoszenia do kwadratu? tylko graficznie?

kasia123: Nie rozumiem, dlaczego wyrzucane z dziedziny zostały −1 i 1, przecież wtedy pod pierwiastkiem mamy 0, a to jest ok

Janek191: Masz wykresy

Janek191: − 1 i 1 należą do dziedziny Odjąłem przedział otwarty, czyli bez −1 i 1.

kasia123: √x4 − x2 ≥ 0 dla dowolnego x ∊ ℛ \ ( − 1, 1) chodzi mi o ten zapis. przeciez pierwiastek zawsze bedzie większy lub równy 0

Adamm: {−1; 1} − zbiór do którego należą jedynie −1 oraz 1 (−1; 1) − zbiór do którego należą wszystkie liczby rzeczywiste x takie że −1<x<1

kasia123: Już to widzę. Dzięki

kasia123: Ponawiam pytanie: jak rozwiązać to bez podnoszenia do kwadratu?

kasia123:

5-latek: tak graficznie mozna rozwiazac bez ppodnoszenia do potegi drugiej

kasia123: dzięki