ekstrema sed: Wyznacz najwieksza wartosc pola prostokata, ktorego dwa wierzcholki leza na paraboli y=x2−4x+4, a dwa pozostale na cieciwie paraboli wyznaczonej przez prosta y=3.

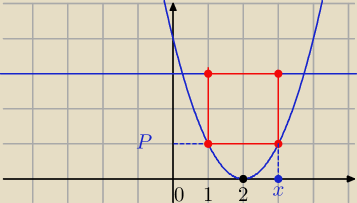
Janek191: P(x) = 2*(x − 2)*( 3 − f(x)) = ( 2 x − 4)*( 3 − ( x² − 4x + 4)) = (2 x − 4)*( − x² + 4 x − 1) P(x) = − 2 x³ + 8 x² − 2 x +4 x² − 16 x + 4 = −2 x³ + 12 x² − 18 x + 4 więc P '(x) = − 6 x² + 24 x − 18 = 0 ⇔ − x² + 4 x − 3 = 0 ⇔ x = 3

sed: ok ale mam pytanie tez mi tak wyszło ale skąd bok x −2 nie mogę pojąć

Janek191: 2*(x − 2) p = 2 − odcięta wierzchołka paraboli

Janek191: x = 2 − oś symetrii paraboli

sed: pomożesz prosze z ostatnim dzis? zaraz wrzuce

sed: w półokrąg o promieniu 1 wpisano prostokąt ABCD, oblicz boki prostokąta tak aby pole było jak największe

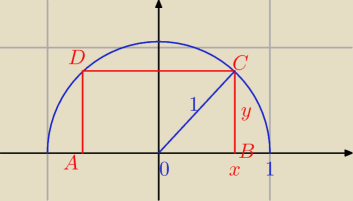
Janek191: Mamy x² + y² = 1 ⇒ y² = 1 − x² ⇒ y = √ 1 − x² , gdzie x ∊ ( 0, 1) Pole prostokąta ABCD P(x) = 2 x*y = 2 x* √1 − x² = √ 4 x² − 4 x⁴ więc

	8 x − 16 x3		2 x − 4 x3
P '(x) =		=		= 0 ⇔ 2 x = 4
	2 √4 x2 − 4 x4		√x2 − x4

x³ ⇔

	1		√2
⇔ 1 = 2 x2 ⇔ x2 =		⇔ x =
	2		2

	√2
Wtedy y =
	2

Boki prostokąta mają długości: a =2 x = √2 b = y = 0,5 √2 ===============