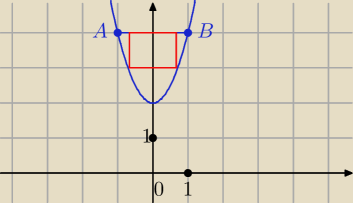
ekstrema sed: Rozważamy wszystkie prostokąty, których dwa wierzchołki leżą na odcinku AB, gdzie A = (−1, 4) i B = (1, 4), a pozostałe dwa na paraboli o równaniu y = 2x² + 2 (zobacz rysunek). Wyznacz wymiary tego z prostokątów, który ma największe pole. Oblicz to pole.

Janek191:

Janek191: P(x) = 2*x*( 4 − f(x)) = 2 x*( 4 − ( 2 x² + 2)) = 2 x*( 2 − 2 x²) = 4 x − 4 x³ więc

	1		√3
P '(x) = 4 − 12 x2 = 0 ⇔ x =		=
	√3		3

Janek191:

	2 √3
a = 2 x =
	3

	√3
b = 4 − f(		)
	3