 Hej mam problem z zadakami, odnośnie przekształceń funkcji wykładniczej, gdyby ktoś mógł
mi to rozwiązać, pomóc :< byłbym mega wdzięczny.
1.1
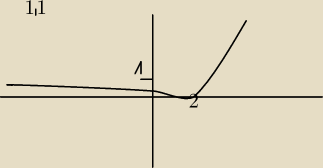
f(x)=|1−2x−2|
Ja to robie tak...
=|−2x−2+1|
I teraz coś, co chyba nie rozumiem czyli co z tą wartością bezwzględną? Zwykle jak miałem tego
typu
wykres to robiłem −f(x) a potem go obracałem i było dobrze (bo ax ⇒ a>0/{1} dla tego
obracałem)
Tutaj mam wartość bezwględna i chyba nie potrafie tego dobrze rozpisać...
Normalnie robilbym tak
−f(x)=2x−2−1 (bah rysuje to co narysowałem na rysunku)
I odwracam, odczytuje to o co proszą i jest oki. Jednak w tym przykładzie jak zerkam do
odpowedzi to okazuje się że mój wykres −f(x) jest tym prawidłowym, nie obracają go.
Wniosek... Mam błąd w rozumowaniu, prosiłbym o rozjaśnienie mroków mojego mózgu, gdyby
ktoś miał czas i ochotę
Hej mam problem z zadakami, odnośnie przekształceń funkcji wykładniczej, gdyby ktoś mógł
mi to rozwiązać, pomóc :< byłbym mega wdzięczny.
1.1
f(x)=|1−2x−2|
Ja to robie tak...
=|−2x−2+1|
I teraz coś, co chyba nie rozumiem czyli co z tą wartością bezwzględną? Zwykle jak miałem tego
typu
wykres to robiłem −f(x) a potem go obracałem i było dobrze (bo ax ⇒ a>0/{1} dla tego
obracałem)
Tutaj mam wartość bezwględna i chyba nie potrafie tego dobrze rozpisać...
Normalnie robilbym tak
−f(x)=2x−2−1 (bah rysuje to co narysowałem na rysunku)
I odwracam, odczytuje to o co proszą i jest oki. Jednak w tym przykładzie jak zerkam do
odpowedzi to okazuje się że mój wykres −f(x) jest tym prawidłowym, nie obracają go.
Wniosek... Mam błąd w rozumowaniu, prosiłbym o rozjaśnienie mroków mojego mózgu, gdyby
ktoś miał czas i ochotę  1.2
Mamy funkcje f(x)=|(12)x−1|
(narysowanie tej funkcji nie stanowi problemu)
Problem to podanie liczby rozwiązań równania w zależności od parametru m f(x)=m
(Nie wiem jak to rozumieć... jakby ktoś mógł mi to wytłumaczyć )
1.2
Mamy funkcje f(x)=|(12)x−1|
(narysowanie tej funkcji nie stanowi problemu)
Problem to podanie liczby rozwiązań równania w zależności od parametru m f(x)=m
(Nie wiem jak to rozumieć... jakby ktoś mógł mi to wytłumaczyć )
| |f(x)−1| | ||
No i nie wiem jak naszkicować wykres funkcji y = | ||
| f(x)−1 |

 f(x)=|1−2x−2|
f(x)=|−2x−2+1|
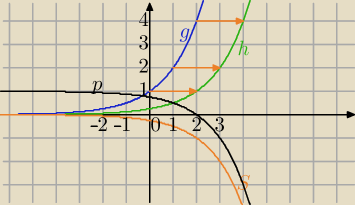
1) g(x)=2x→T[2,0]⇒otrzymujesz wykres h(x)=2x−2→SOX otrzymujez wykres :
⇒s(x)=−2x−2→teraz →T[0,1] ⇔p(x)=1−2x−2
Teraz narysuję w nowym układzie wsp.
f(x)=|1−2x−2|
f(x)=|−2x−2+1|
1) g(x)=2x→T[2,0]⇒otrzymujesz wykres h(x)=2x−2→SOX otrzymujez wykres :
⇒s(x)=−2x−2→teraz →T[0,1] ⇔p(x)=1−2x−2
Teraz narysuję w nowym układzie wsp.
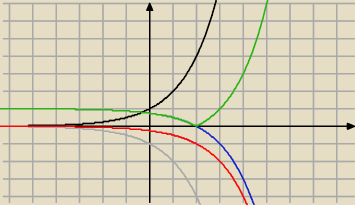 y= |1−2x−2|
1 rysujesz y= 2x (czarny
2 odbijasz y= 2x wzgledem osi OX i masz y=−2x (szary
3. y=−2x przesuwasz o 2 jednostki w prawo i masz y=−2x−2 (czerwony
4 y=−2x−2 przesuwasz po osi OY o jedna jedostke w gore i masz y=−2x−1+1 (czyli 1−2x−2
(nie bieski
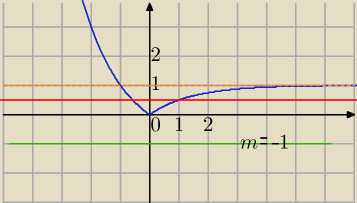
Teraz y=|1−2x−2 | (zielony
na wykres y=1−2x−2 nakladsz wartosc bezwzgledna (wiec to co pod osia oX wedruje na gore
to co nad osia zostaje .
y= |1−2x−2|
1 rysujesz y= 2x (czarny
2 odbijasz y= 2x wzgledem osi OX i masz y=−2x (szary
3. y=−2x przesuwasz o 2 jednostki w prawo i masz y=−2x−2 (czerwony
4 y=−2x−2 przesuwasz po osi OY o jedna jedostke w gore i masz y=−2x−1+1 (czyli 1−2x−2
(nie bieski
Teraz y=|1−2x−2 | (zielony
na wykres y=1−2x−2 nakladsz wartosc bezwzgledna (wiec to co pod osia oX wedruje na gore
to co nad osia zostaje .
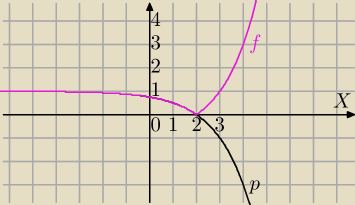 p(x)=1−2x−2→SOX dla tej części wykresu co leży pod osią ⇒
f(x)=|1−2x−2|
p(x)=1−2x−2→SOX dla tej części wykresu co leży pod osią ⇒
f(x)=|1−2x−2|
 Nie widzialem Twojego wpisu
Nie widzialem Twojego wpisu
 2)
2)
| 1 | ||
f(x)=|( | )x−1| | |
| 2 |
| |f(x)−1| | ||
y= | ||
| f(x)−1 |
 Dziękuje Milo i Tobie 5−latku, pomogliście mi już wszystko jasne jeżeli chodzi o 1.1
Dziękuje Milo i Tobie 5−latku, pomogliście mi już wszystko jasne jeżeli chodzi o 1.1  Ps. ^^ Dobrze, że napisałeś swój post 5−latku bo z początku nie za bardzo zrozumiłem o co
chodzi Mili, za to Twoj post zrozumiałem do strzału
Ps. ^^ Dobrze, że napisałeś swój post 5−latku bo z początku nie za bardzo zrozumiłem o co
chodzi Mili, za to Twoj post zrozumiałem do strzału  I po zerknięciu raz jeszcze po tym
jak przeczytałem Twój post na post Mili, doszło do mnie, o co chodzi. Toszkę za głupi jestem
jeszcze (mam nadzieję że jeszcze), żeby tak szybko łapać taki śliczny język matematyczny
jakim Mila się posłużyła
I po zerknięciu raz jeszcze po tym
jak przeczytałem Twój post na post Mili, doszło do mnie, o co chodzi. Toszkę za głupi jestem
jeszcze (mam nadzieję że jeszcze), żeby tak szybko łapać taki śliczny język matematyczny
jakim Mila się posłużyła  Tak że doceniam, obie odpowiedzi. Dzięki raz jeszcze.
Tak że doceniam, obie odpowiedzi. Dzięki raz jeszcze.
| 1 | ||
f(x)=|( | )x−1| | |
| 2 |
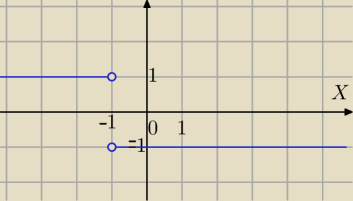
| |||||||||||
y= | |||||||||||
|
| 1 | ||
|( | )x−1|−1≠0 | |
| 2 |
| 1 | ||
|( | )x−1|−1>0 | |
| 2 |
| 1 | ||
|( | )x−1|>1⇔ | |
| 2 |
| 1 | 1 | |||
( | )x−1<−1 lub ( | )x−1>1 | ||
| 2 | 2 |
| 1 | 1 | |||
( | )x<0 sprzeczność lub ( | )x>2⇔ | ||
| 2 | 2 |
| 1 | 1 | |||
( | )x>( | )−1 ⇔x<−1 | ||
| 2 | 2 |
| 1 | ||
y=−1 dla |( | )x−1|−1<0⇔ | |
| 2 |
| 1 | ||
|( | )x−1|<1 | |
| 2 |
| 1 | ||
−1<( | )x−1<1 / +1 | |
| 2 |
| 1 | ||
0<( | )x<2 | |
| 2 |
| 1 | 1 | |||
( | )x< | )−1⇔ | ||
| 2 | 2 |
| 1 | ||
Chyba rozumiem, choć mam pytanie odnośnie tego 2 |( | )x−1|>0 rozpatrzamy to w ten sposób | |
| 2 |
 Kurcze muszę sobie chyba powtórzyć jak działa wartość bezwzględna .
Dzięki milo za pomoc
Kurcze muszę sobie chyba powtórzyć jak działa wartość bezwzględna .
Dzięki milo za pomoc  Pozdrawiam Michał
Pozdrawiam Michał
